Statistical and Computational Guarantees of Lloyd's Algorithm and its Variants
Paper and Code
Dec 07, 2016


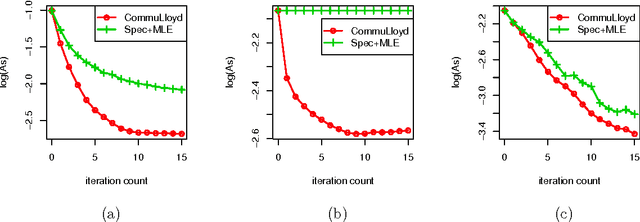
Clustering is a fundamental problem in statistics and machine learning. Lloyd's algorithm, proposed in 1957, is still possibly the most widely used clustering algorithm in practice due to its simplicity and empirical performance. However, there has been little theoretical investigation on the statistical and computational guarantees of Lloyd's algorithm. This paper is an attempt to bridge this gap between practice and theory. We investigate the performance of Lloyd's algorithm on clustering sub-Gaussian mixtures. Under an appropriate initialization for labels or centers, we show that Lloyd's algorithm converges to an exponentially small clustering error after an order of $\log n$ iterations, where $n$ is the sample size. The error rate is shown to be minimax optimal. For the two-mixture case, we only require the initializer to be slightly better than random guess. In addition, we extend the Lloyd's algorithm and its analysis to community detection and crowdsourcing, two problems that have received a lot of attention recently in statistics and machine learning. Two variants of Lloyd's algorithm are proposed respectively for community detection and crowdsourcing. On the theoretical side, we provide statistical and computational guarantees of the two algorithms, and the results improve upon some previous signal-to-noise ratio conditions in literature for both problems. Experimental results on simulated and real data sets demonstrate competitive performance of our algorithms to the state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge