Stationary Behavior of Constant Stepsize SGD Type Algorithms: An Asymptotic Characterization

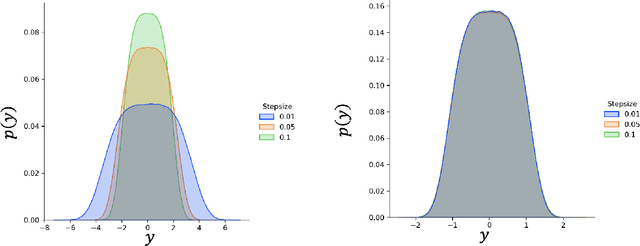
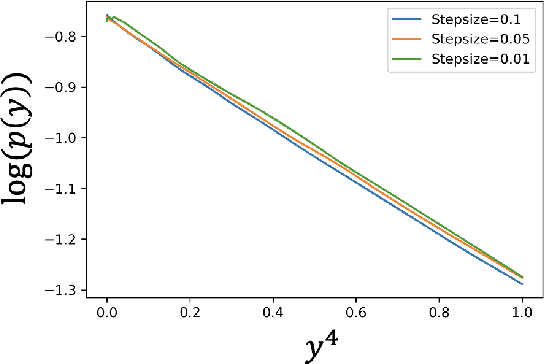
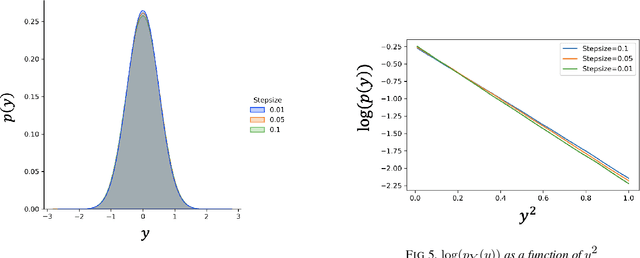
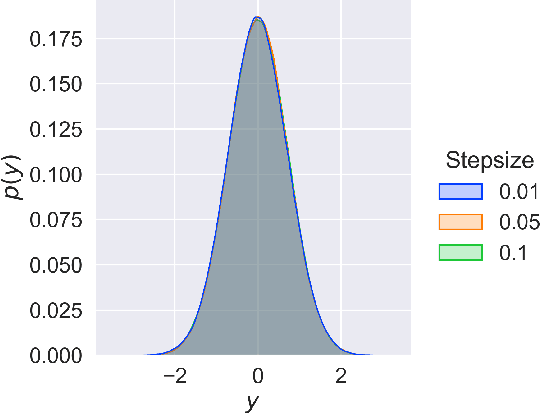
Stochastic approximation (SA) and stochastic gradient descent (SGD) algorithms are work-horses for modern machine learning algorithms. Their constant stepsize variants are preferred in practice due to fast convergence behavior. However, constant step stochastic iterative algorithms do not converge asymptotically to the optimal solution, but instead have a stationary distribution, which in general cannot be analytically characterized. In this work, we study the asymptotic behavior of the appropriately scaled stationary distribution, in the limit when the constant stepsize goes to zero. Specifically, we consider the following three settings: (1) SGD algorithms with smooth and strongly convex objective, (2) linear SA algorithms involving a Hurwitz matrix, and (3) nonlinear SA algorithms involving a contractive operator. When the iterate is scaled by $1/\sqrt{\alpha}$, where $\alpha$ is the constant stepsize, we show that the limiting scaled stationary distribution is a solution of an integral equation. Under a uniqueness assumption (which can be removed in certain settings) on this equation, we further characterize the limiting distribution as a Gaussian distribution whose covariance matrix is the unique solution of a suitable Lyapunov equation. For SA algorithms beyond these cases, our numerical experiments suggest that unlike central limit theorem type results: (1) the scaling factor need not be $1/\sqrt{\alpha}$, and (2) the limiting distribution need not be Gaussian. Based on the numerical study, we come up with a formula to determine the right scaling factor, and make insightful connection to the Euler-Maruyama discretization scheme for approximating stochastic differential equations.