Standard Steady State Genetic Algorithms Can Hillclimb Faster than Mutation-only Evolutionary Algorithms
Paper and Code
Aug 25, 2017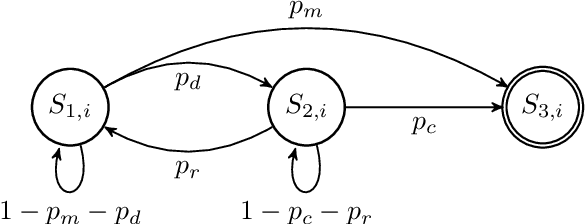
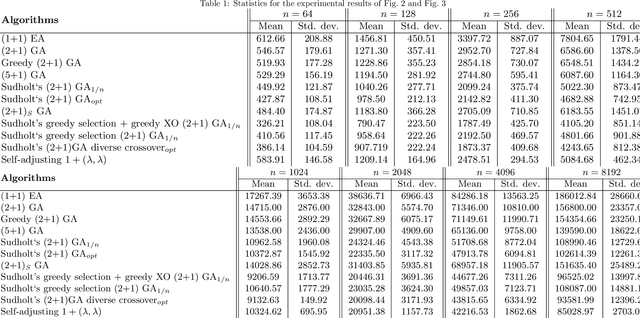
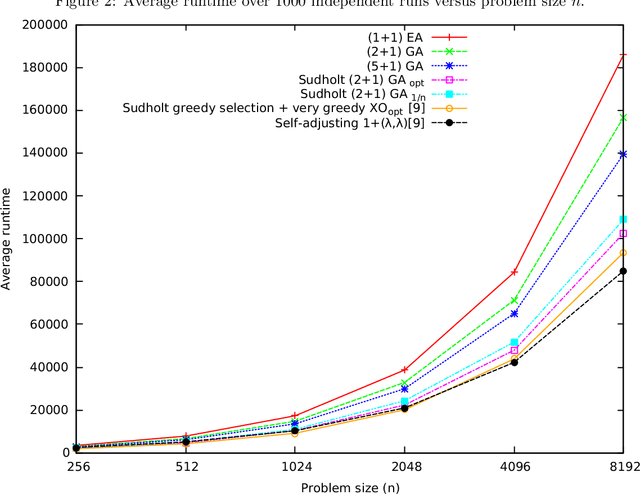

Explaining to what extent the real power of genetic algorithms lies in the ability of crossover to recombine individuals into higher quality solutions is an important problem in evolutionary computation. In this paper we show how the interplay between mutation and crossover can make genetic algorithms hillclimb faster than their mutation-only counterparts. We devise a Markov Chain framework that allows to rigorously prove an upper bound on the runtime of standard steady state genetic algorithms to hillclimb the OneMax function. The bound establishes that the steady-state genetic algorithms are 25% faster than all standard bit mutation-only evolutionary algorithms with static mutation rate up to lower order terms for moderate population sizes. The analysis also suggests that larger populations may be faster than populations of size 2. We present a lower bound for a greedy (2+1) GA that matches the upper bound for populations larger than 2, rigorously proving that 2 individuals cannot outperform larger population sizes under greedy selection and greedy crossover up to lower order terms. In complementary experiments the best population size is greater than 2 and the greedy genetic algorithms are faster than standard ones, further suggesting that the derived lower bound also holds for the standard steady state (2+1) GA.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge