Stacking Factorizing Partitioned Expressions in Hybrid Bayesian Network Models
Paper and Code
Feb 23, 2024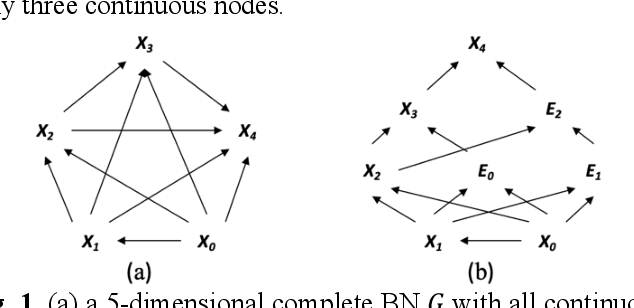
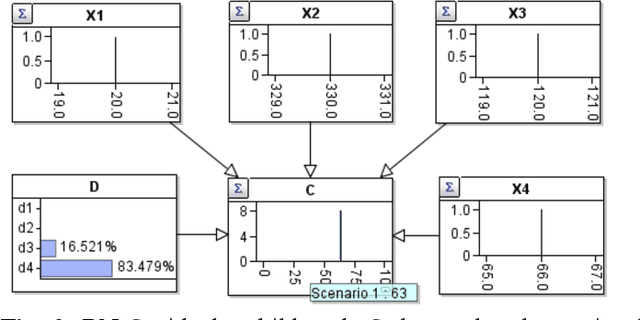
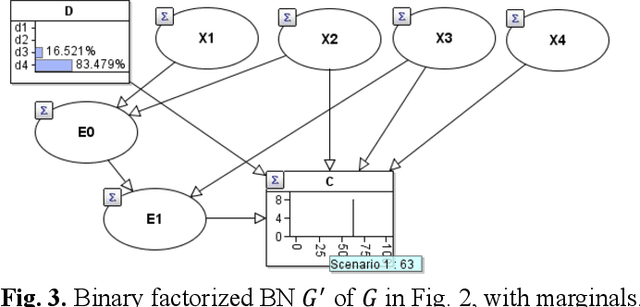
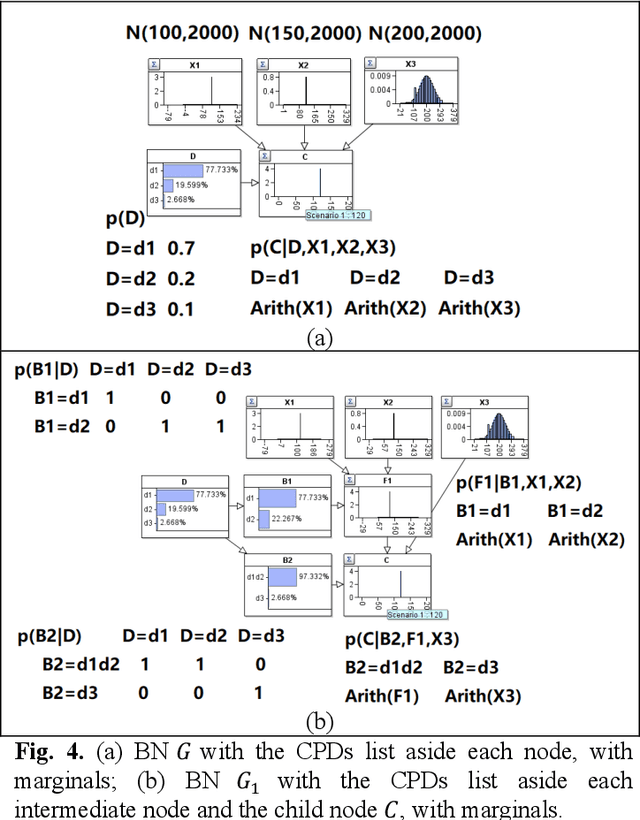
Hybrid Bayesian networks (HBN) contain complex conditional probabilistic distributions (CPD) specified as partitioned expressions over discrete and continuous variables. The size of these CPDs grows exponentially with the number of parent nodes when using discrete inference, resulting in significant inefficiency. Normally, an effective way to reduce the CPD size is to use a binary factorization (BF) algorithm to decompose the statistical or arithmetic functions in the CPD by factorizing the number of connected parent nodes to sets of size two. However, the BF algorithm was not designed to handle partitioned expressions. Hence, we propose a new algorithm called stacking factorization (SF) to decompose the partitioned expressions. The SF algorithm creates intermediate nodes to incrementally reconstruct the densities in the original partitioned expression, allowing no more than two continuous parent nodes to be connected to each child node in the resulting HBN. SF can be either used independently or combined with the BF algorithm. We show that the SF+BF algorithm significantly reduces the CPD size and contributes to lowering the tree-width of a model, thus improving efficiency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge