Stabilizing Training of Generative Adversarial Nets via Langevin Stein Variational Gradient Descent
Paper and Code
Apr 22, 2020
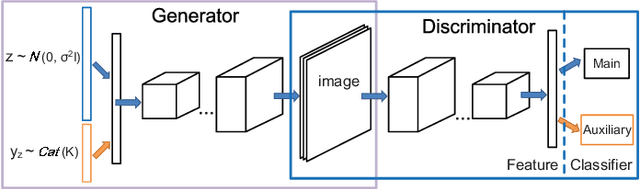

Generative adversarial networks (GANs), famous for the capability of learning complex underlying data distribution, are however known to be tricky in the training process, which would probably result in mode collapse or performance deterioration. Current approaches of dealing with GANs' issues almost utilize some practical training techniques for the purpose of regularization, which on the other hand undermines the convergence and theoretical soundness of GAN. In this paper, we propose to stabilize GAN training via a novel particle-based variational inference -- Langevin Stein variational gradient descent (LSVGD), which not only inherits the flexibility and efficiency of original SVGD but aims to address its instability issues by incorporating an extra disturbance into the update dynamics. We further demonstrate that by properly adjusting the noise variance, LSVGD simulates a Langevin process whose stationary distribution is exactly the target distribution. We also show that LSVGD dynamics has an implicit regularization which is able to enhance particles' spread-out and diversity. At last we present an efficient way of applying particle-based variational inference on a general GAN training procedure no matter what loss function is adopted. Experimental results on one synthetic dataset and three popular benchmark datasets -- Cifar-10, Tiny-ImageNet and CelebA validate that LSVGD can remarkably improve the performance and stability of various GAN models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge