SPRITE: A Response Model For Multiple Choice Testing
Paper and Code
Jan 12, 2015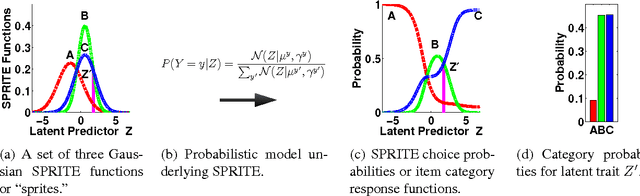
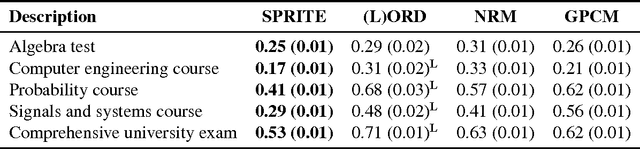
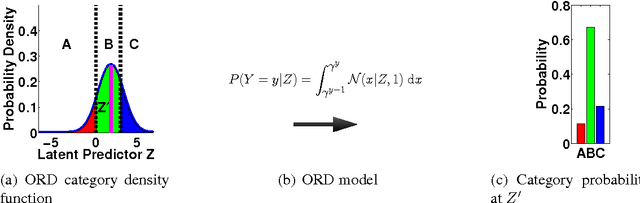
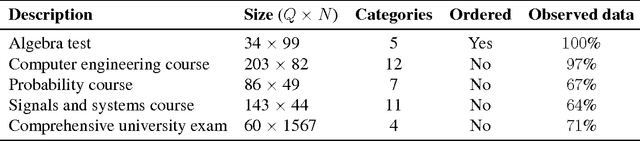
Item response theory (IRT) models for categorical response data are widely used in the analysis of educational data, computerized adaptive testing, and psychological surveys. However, most IRT models rely on both the assumption that categories are strictly ordered and the assumption that this ordering is known a priori. These assumptions are impractical in many real-world scenarios, such as multiple-choice exams where the levels of incorrectness for the distractor categories are often unknown. While a number of results exist on IRT models for unordered categorical data, they tend to have restrictive modeling assumptions that lead to poor data fitting performance in practice. Furthermore, existing unordered categorical models have parameters that are difficult to interpret. In this work, we propose a novel methodology for unordered categorical IRT that we call SPRITE (short for stochastic polytomous response item model) that: (i) analyzes both ordered and unordered categories, (ii) offers interpretable outputs, and (iii) provides improved data fitting compared to existing models. We compare SPRITE to existing item response models and demonstrate its efficacy on both synthetic and real-world educational datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge