Sphere Neural-Networks for Rational Reasoning
Paper and Code
Mar 22, 2024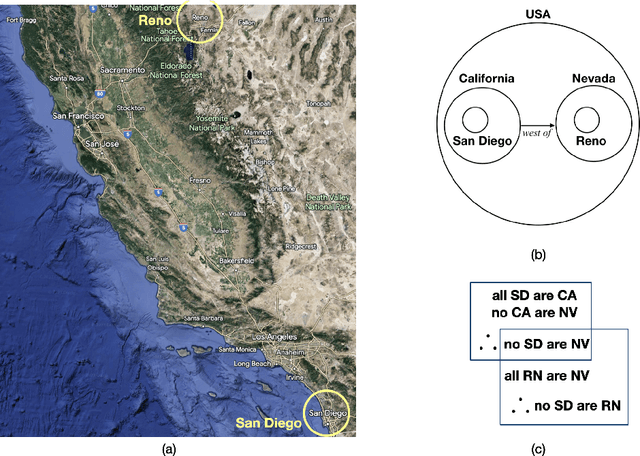
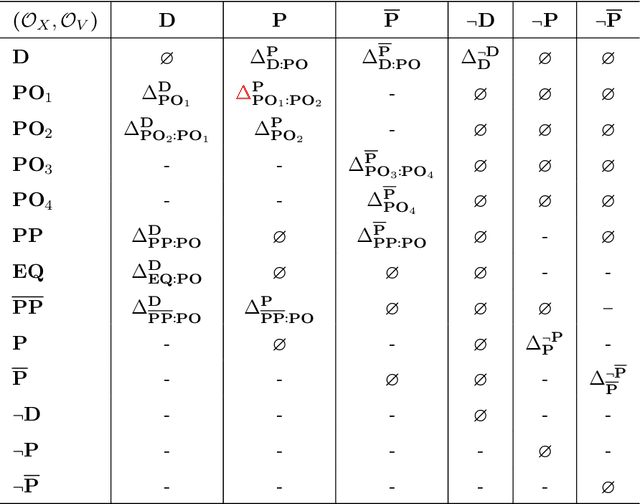
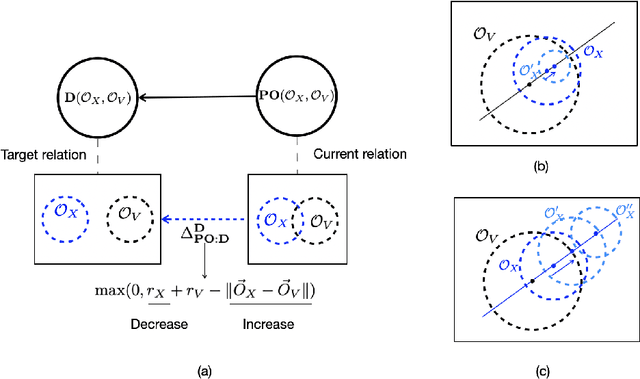
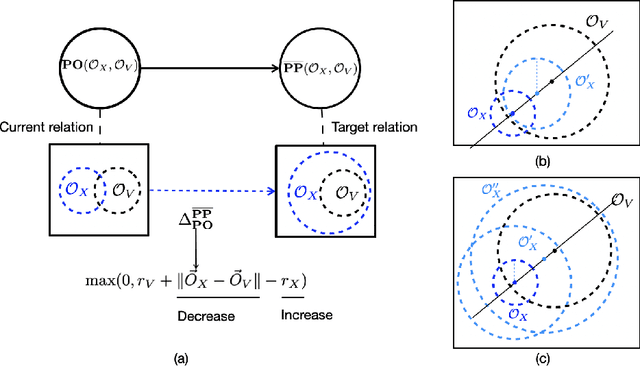
The success of Large Language Models (LLMs), e.g., ChatGPT, is witnessed by their planetary popularity, their capability of human-like question-answering, and also by their steadily improved reasoning performance. However, it remains unclear whether LLMs reason. It is an open problem how traditional neural networks can be qualitatively extended to go beyond the statistic paradigm and achieve high-level cognition. Here, we present a minimalist qualitative extension by generalising computational building blocks from vectors to spheres. We propose Sphere Neural Networks (SphNNs) for human-like reasoning through model construction and inspection, and develop SphNN for syllogistic reasoning, a microcosm of human rationality. Instead of training data, SphNN uses a neuro-symbolic transition map of neighbourhood spatial relations to guide transformations from the current sphere configuration towards the target. SphNN is the first neural model that can determine the validity of long-chained syllogistic reasoning in one epoch by constructing sphere configurations as Euler diagrams, with the worst computational complexity of O(N^2). SphNN can evolve into various types of reasoning, such as spatio-temporal reasoning, logical reasoning with negation and disjunction, event reasoning, neuro-symbolic reasoning, and humour understanding (the highest level of cognition). All these suggest a new kind of Herbert A. Simon's scissors with two neural blades. SphNNs will tremendously enhance interdisciplinary collaborations to develop the two neural blades and realise deterministic neural reasoning and human-bounded rationality and elevate LLMs to reliable psychological AI. This work suggests that the non-zero radii of spheres are the missing components that prevent traditional deep-learning systems from reaching the realm of rational reasoning and cause LLMs to be trapped in the swamp of hallucination.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge