Speeding up and reducing memory usage for scientific machine learning via mixed precision
Paper and Code
Jan 30, 2024
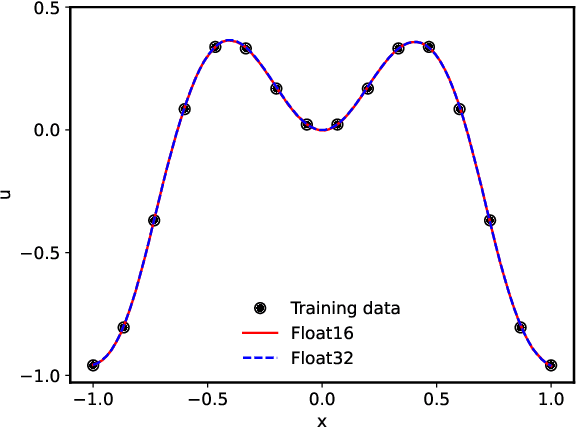

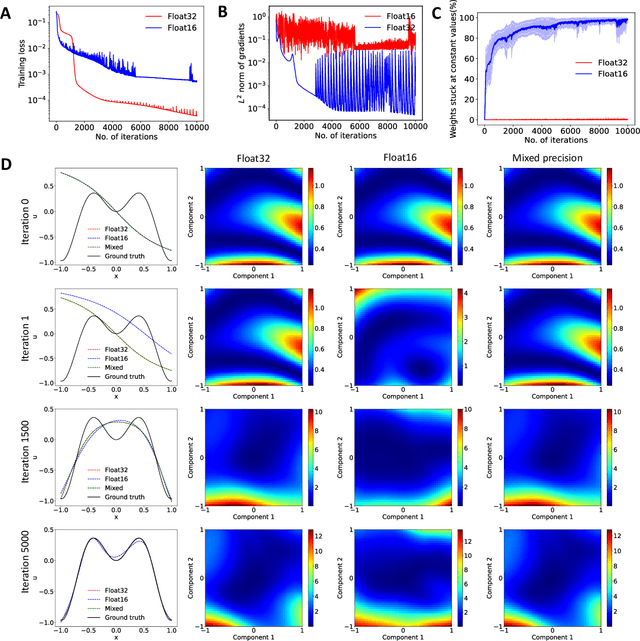
Scientific machine learning (SciML) has emerged as a versatile approach to address complex computational science and engineering problems. Within this field, physics-informed neural networks (PINNs) and deep operator networks (DeepONets) stand out as the leading techniques for solving partial differential equations by incorporating both physical equations and experimental data. However, training PINNs and DeepONets requires significant computational resources, including long computational times and large amounts of memory. In search of computational efficiency, training neural networks using half precision (float16) rather than the conventional single (float32) or double (float64) precision has gained substantial interest, given the inherent benefits of reduced computational time and memory consumed. However, we find that float16 cannot be applied to SciML methods, because of gradient divergence at the start of training, weight updates going to zero, and the inability to converge to a local minima. To overcome these limitations, we explore mixed precision, which is an approach that combines the float16 and float32 numerical formats to reduce memory usage and increase computational speed. Our experiments showcase that mixed precision training not only substantially decreases training times and memory demands but also maintains model accuracy. We also reinforce our empirical observations with a theoretical analysis. The research has broad implications for SciML in various computational applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge