Spectral Modes of Network Dynamics Reveal Increased Informational Complexity Near Criticality
Paper and Code
Jul 05, 2017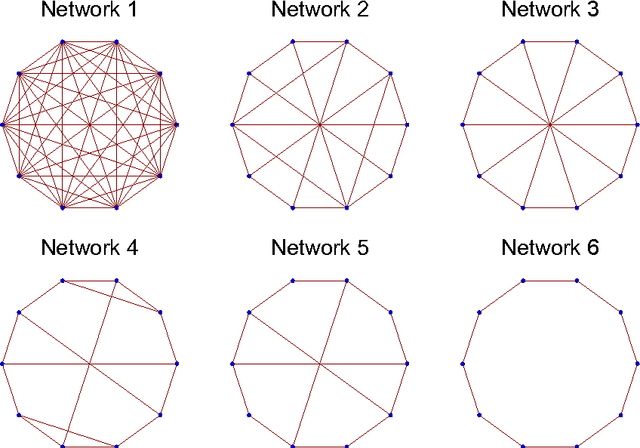
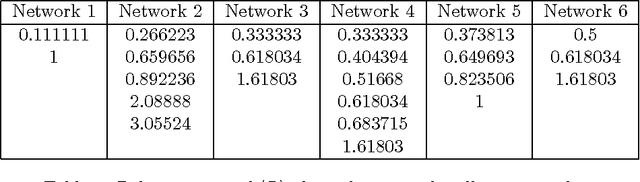
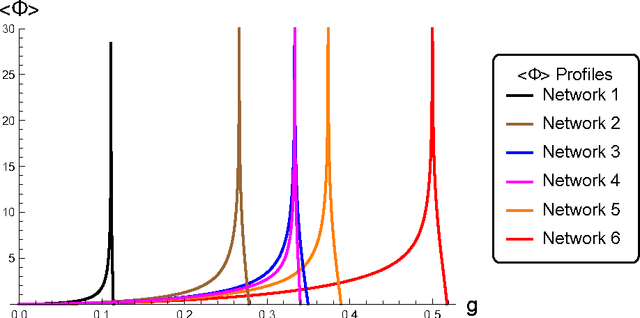
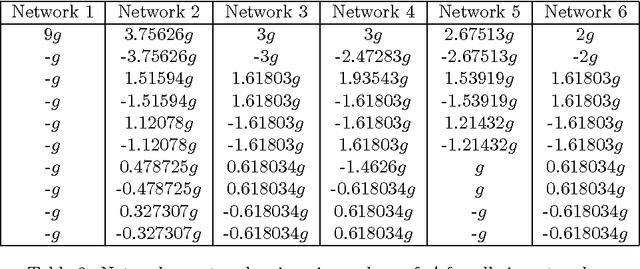
What does the informational complexity of dynamical networked systems tell us about intrinsic mechanisms and functions of these complex systems? Recent complexity measures such as integrated information have sought to operationalize this problem taking a whole-versus-parts perspective, wherein one explicitly computes the amount of information generated by a network as a whole over and above that generated by the sum of its parts during state transitions. While several numerical schemes for estimating network integrated information exist, it is instructive to pursue an analytic approach that computes integrated information as a function of network weights. Our formulation of integrated information uses a Kullback-Leibler divergence between the multi-variate distribution on the set of network states versus the corresponding factorized distribution over its parts. Implementing stochastic Gaussian dynamics, we perform computations for several prototypical network topologies. Our findings show increased informational complexity near criticality, which remains consistent across network topologies. Spectral decomposition of the system's dynamics reveals how informational complexity is governed by eigenmodes of both, the network's covariance and adjacency matrices. We find that as the dynamics of the system approach criticality, high integrated information is exclusively driven by the eigenmode corresponding to the leading eigenvalue of the covariance matrix, while sub-leading modes get suppressed. The implication of this result is that it might be favorable for complex dynamical networked systems such as the human brain or communication systems to operate near criticality so that efficient information integration might be achieved.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge