Spectral inference for large Stochastic Blockmodels with nodal covariates

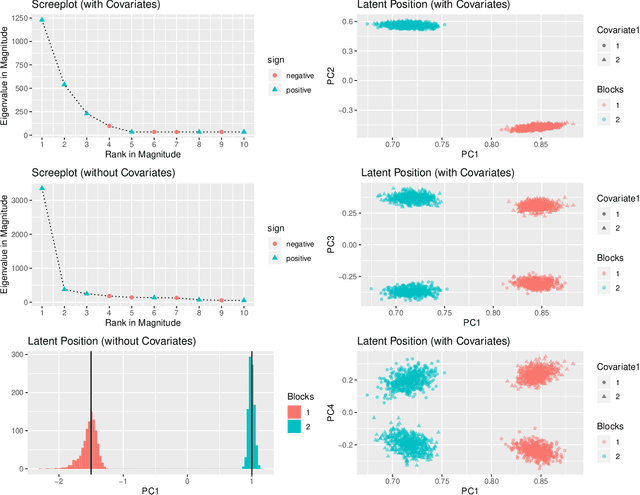
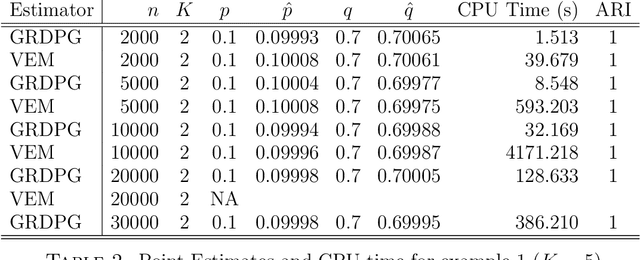
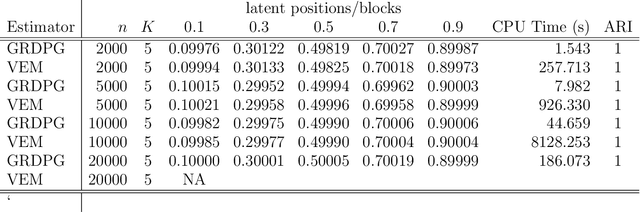
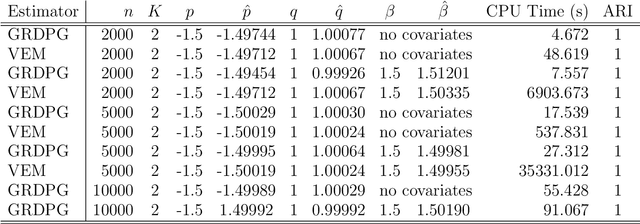
In many applications of network analysis, it is important to distinguish between observed and unobserved factors affecting network structure. To this end, we develop spectral estimators for both unobserved blocks and the effect of covariates in stochastic blockmodels. Our main strategy is to reformulate the stochastic blockmodel estimation problem as recovery of latent positions in a generalized random dot product graph. On the theoretical side, we establish asymptotic normality of our estimators for the subsequent purpose of performing inference. On the applied side, we show that computing our estimator is much faster than standard variational expectation--maximization algorithms and scales well for large networks. The results in this paper provide a foundation to estimate the effect of observed covariates as well as unobserved latent community structure on the probability of link formation in networks.