Spatial motion planning with Pythagorean Hodograph curves
Paper and Code
Sep 04, 2022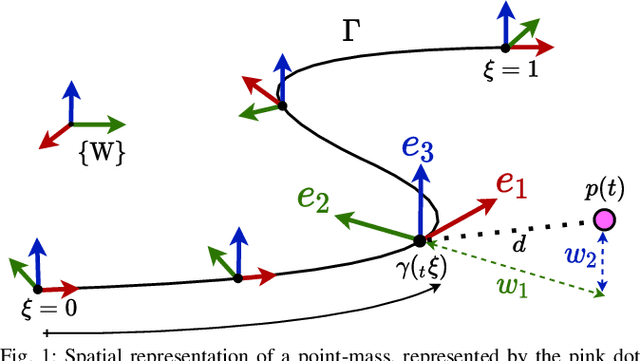

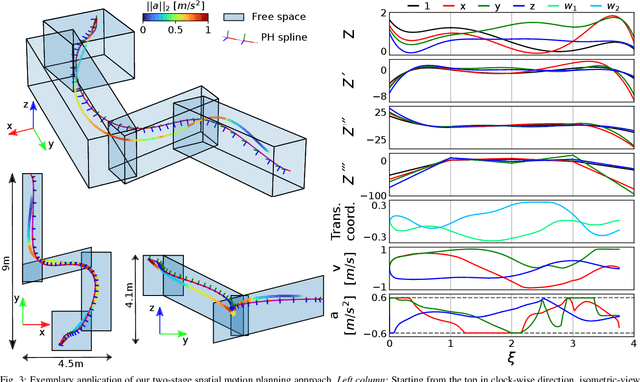
This paper presents a two-stage prediction-based control scheme for embedding the environment's geometric properties into a collision-free Pythagorean Hodograph spline, and subsequently finding the optimal path within the parameterized free space. The ingredients of this approach are twofold: First, we present a novel spatial path parameterization applicable to any arbitrary curve without prior assumptions in its adapted frame. Second, we identify the appropriateness of Pythagorean Hodograph curves for a compact and continuous definition of the path-parametric functions required by the presented spatial model. This dual-stage formulation results in a motion planning approach, where the geometric properties of the environment arise as states of the prediction model. Thus, the presented method is attractive for motion planning in dense environments. The efficacy of the approach is evaluated according to an illustrative example.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge