Sparsity in Multivariate Extremes with Applications to Anomaly Detection

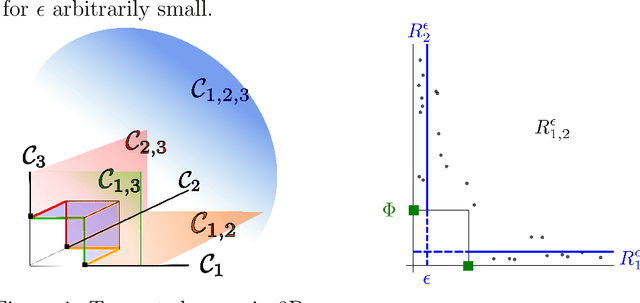
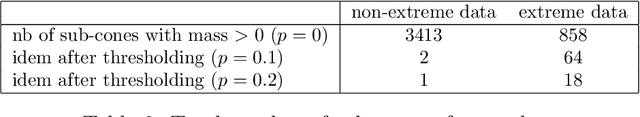
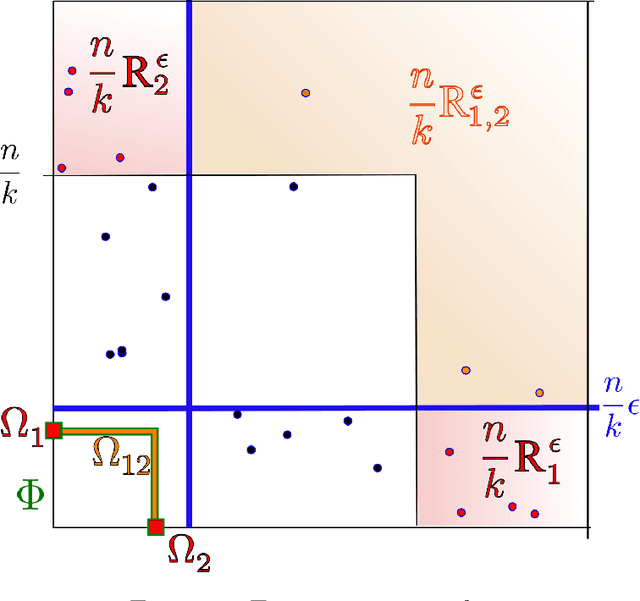
Capturing the dependence structure of multivariate extreme events is a major concern in many fields involving the management of risks stemming from multiple sources, e.g. portfolio monitoring, insurance, environmental risk management and anomaly detection. One convenient (non-parametric) characterization of extremal dependence in the framework of multivariate Extreme Value Theory (EVT) is the angular measure, which provides direct information about the probable 'directions' of extremes, that is, the relative contribution of each feature/coordinate of the 'largest' observations. Modeling the angular measure in high dimensional problems is a major challenge for the multivariate analysis of rare events. The present paper proposes a novel methodology aiming at exhibiting a sparsity pattern within the dependence structure of extremes. This is done by estimating the amount of mass spread by the angular measure on representative sets of directions, corresponding to specific sub-cones of $R^d\_+$. This dimension reduction technique paves the way towards scaling up existing multivariate EVT methods. Beyond a non-asymptotic study providing a theoretical validity framework for our method, we propose as a direct application a --first-- anomaly detection algorithm based on multivariate EVT. This algorithm builds a sparse 'normal profile' of extreme behaviours, to be confronted with new (possibly abnormal) extreme observations. Illustrative experimental results provide strong empirical evidence of the relevance of our approach.