Sparse Stochastic Zeroth-Order Optimization with an Application to Bandit Structured Prediction
Paper and Code
Jul 31, 2018
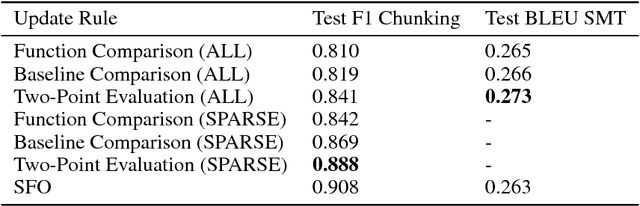

Stochastic zeroth-order (SZO), or gradient-free, optimization allows to optimize arbitrary functions by relying only on function evaluations under parameter perturbations, however, the iteration complexity of SZO methods suffers a factor proportional to the dimensionality of the perturbed function. We show that in scenarios with natural sparsity patterns as in structured prediction applications, this factor can be reduced to the expected number of active features over input-output pairs. We give a general proof that applies sparse SZO optimization to Lipschitz-continuous, nonconvex, stochastic objectives, and present an experimental evaluation on linear bandit structured prediction tasks with sparse word-based feature representations that confirm our theoretical results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge