Sparse-SignSGD with Majority Vote for Communication-Efficient Distributed Learning
Paper and Code
Feb 15, 2023

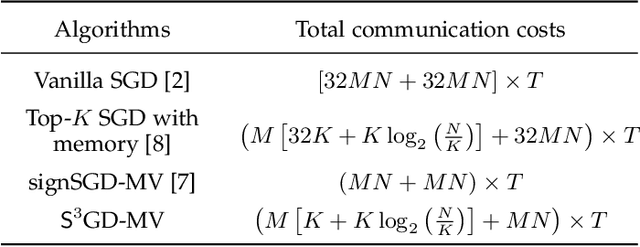

The training efficiency of complex deep learning models can be significantly improved through the use of distributed optimization. However, this process is often hindered by a large amount of communication cost between workers and a parameter server during iterations. To address this bottleneck, in this paper, we present a new communication-efficient algorithm that offers the synergistic benefits of both sparsification and sign quantization, called ${\sf S}^3$GD-MV. The workers in ${\sf S}^3$GD-MV select the top-$K$ magnitude components of their local gradient vector and only send the signs of these components to the server. The server then aggregates the signs and returns the results via a majority vote rule. Our analysis shows that, under certain mild conditions, ${\sf S}^3$GD-MV can converge at the same rate as signSGD while significantly reducing communication costs, if the sparsification parameter $K$ is properly chosen based on the number of workers and the size of the deep learning model. Experimental results using both independent and identically distributed (IID) and non-IID datasets demonstrate that the ${\sf S}^3$GD-MV attains higher accuracy than signSGD, significantly reducing communication costs. These findings highlight the potential of ${\sf S}^3$GD-MV as a promising solution for communication-efficient distributed optimization in deep learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge