Sparse multiresolution representations with adaptive kernels
Paper and Code
May 07, 2019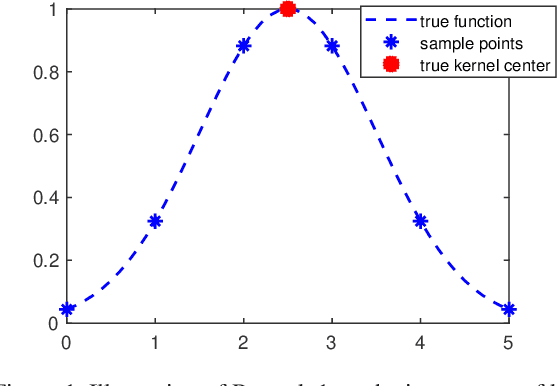
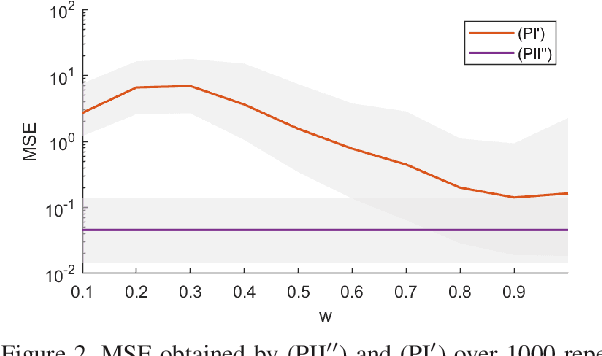
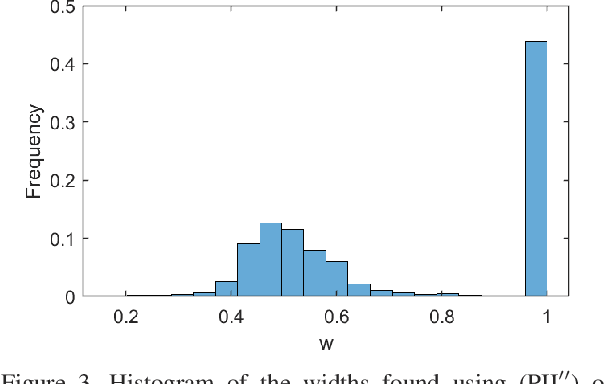
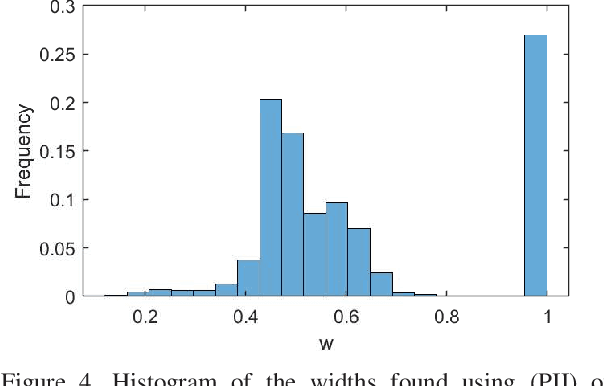
Reproducing kernel Hilbert spaces (RKHSs) are key elements of many non-parametric tools successfully used in signal processing, statistics, and machine learning. In this work, we aim to address three issues of the classical RKHS based techniques. First, they require the RKHS to be known a priori, which is unrealistic in many applications. Furthermore, the choice of RKHS affects the shape and smoothness of the solution, thus impacting its performance. Second, RKHSs are ill-equipped to deal with heterogeneous degrees of smoothness, i.e., with functions that are smooth in some parts of their domain but vary rapidly in others. Finally, the computational complexity of evaluating the solution of these methods grows with the number of data points, rendering these techniques infeasible for many applications. Though kernel learning, local kernel adaptation, and sparsity have been used to address these issues, many of these approaches are computationally intensive or forgo optimality guarantees. We tackle these problems by leveraging a novel integral representation of functions in RKHSs that allows for arbitrary centers and different kernels at each center. To address the complexity issues, we then write the function estimation problem as a sparse functional program that explicitly minimizes the support of the representation leading to low complexity solutions. Despite their non-convexity and infinite dimensionality, we show these problems can be solved exactly and efficiently by leveraging duality, and we illustrate this new approach in simulated and real data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge