Sparse Channel Estimation in Wideband Systems with Geometric Sequence Decomposition
Paper and Code
Apr 09, 2021

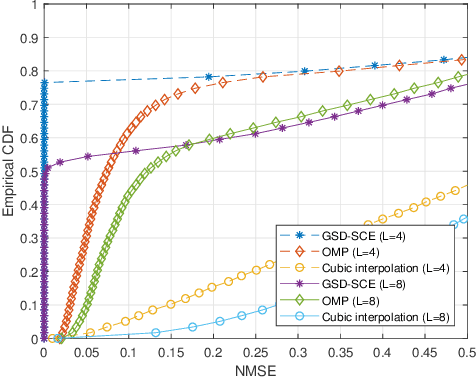
The sparsity of multipaths in wideband channel has motivated the use of compressed sensing for channel estimation. In this letter, we propose an entirely different approach to sparse channel estimation. We exploit the fact that $L$ taps of channel impulse response in time domain constitute a non-orthogonal superposition of $L$ geometric sequences in frequency domain. This converts the channel estimation problem into the extraction of the parameters of geometric sequences. Notably, the proposed scheme achieves the error-free estimation of the whole bandwidth with a few pilot symbols if the excess delay is bounded to a certain value.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge