Sorting by Swaps with Noisy Comparisons
Paper and Code
Mar 12, 2018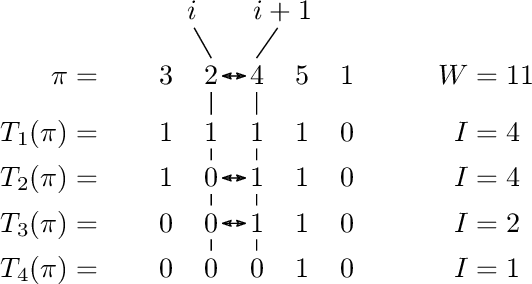
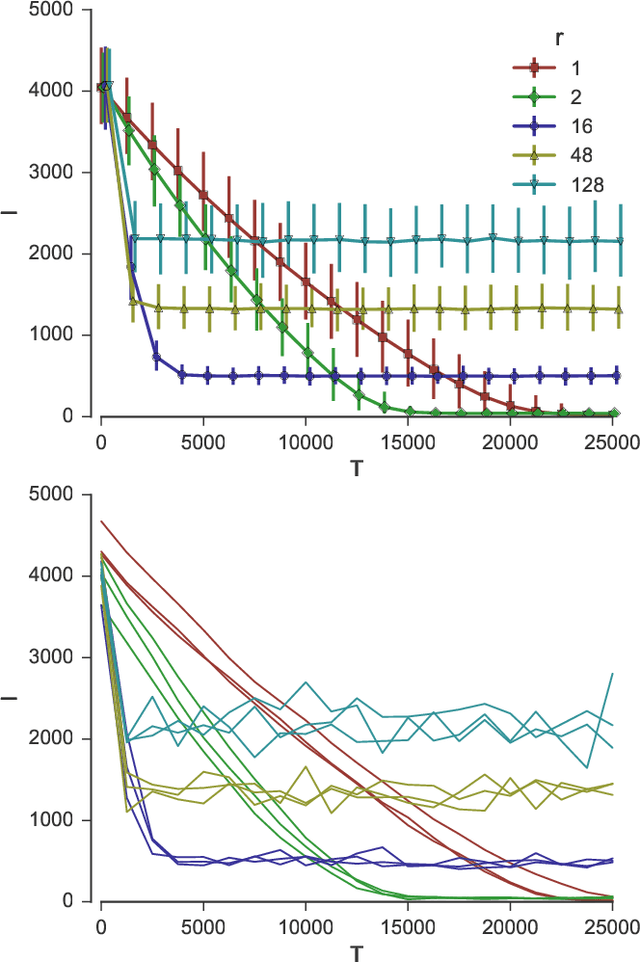
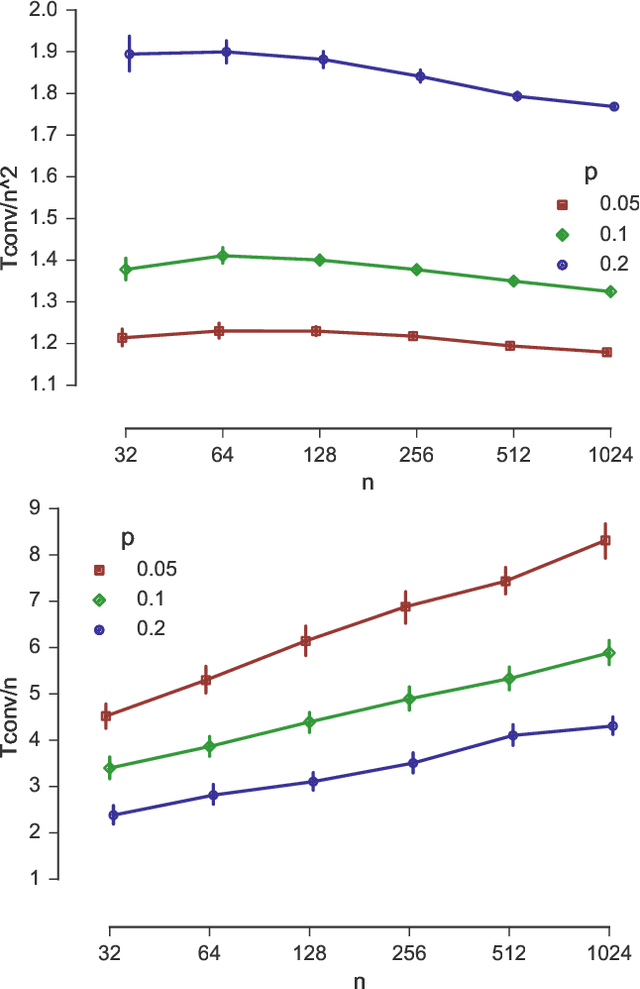
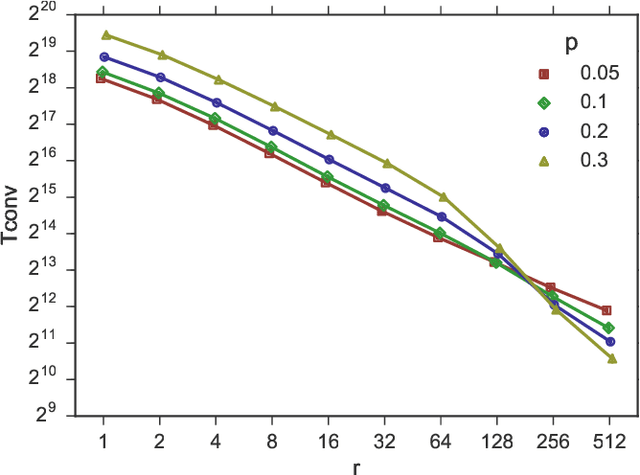
We study sorting of permutations by random swaps if each comparison gives the wrong result with some fixed probability $p<1/2$. We use this process as prototype for the behaviour of randomized, comparison-based optimization heuristics in the presence of noisy comparisons. As quality measure, we compute the expected fitness of the stationary distribution. To measure the runtime, we compute the minimal number of steps after which the average fitness approximates the expected fitness of the stationary distribution. We study the process where in each round a random pair of elements at distance at most $r$ are compared. We give theoretical results for the extreme cases $r=1$ and $r=n$, and experimental results for the intermediate cases. We find a trade-off between faster convergence (for large $r$) and better quality of the solution after convergence (for small $r$).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge