Solving large-scale MEG/EEG source localization and functional connectivity problems simultaneously using state-space models
Paper and Code
Aug 26, 2022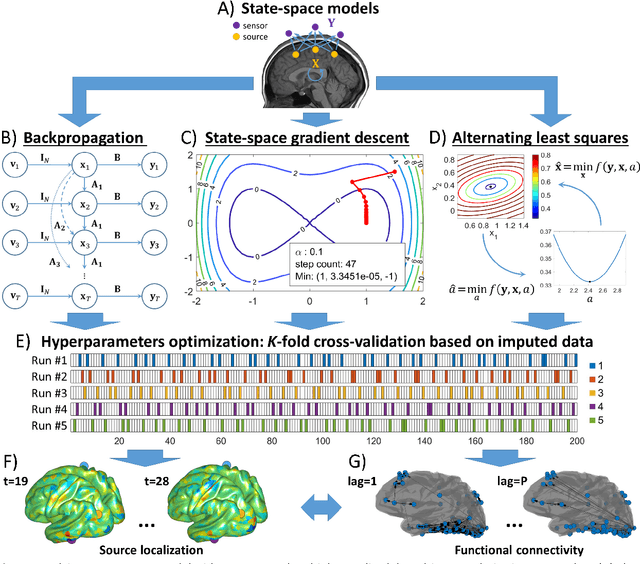
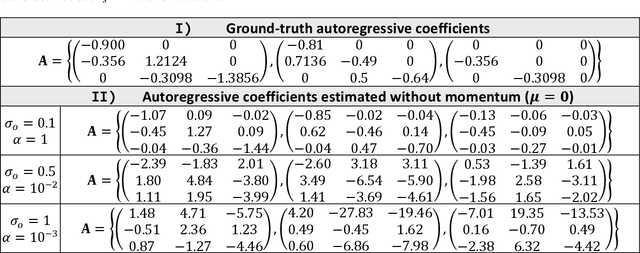
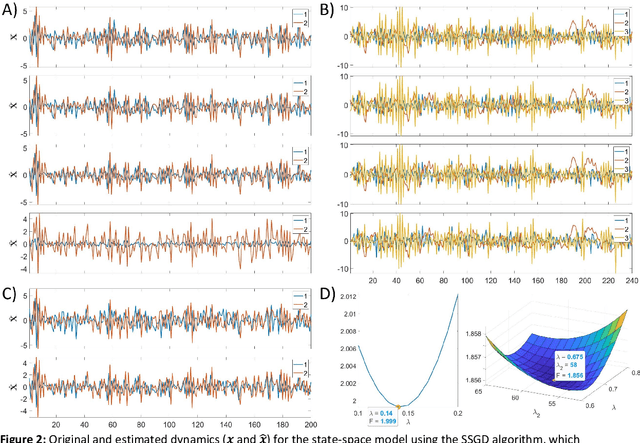
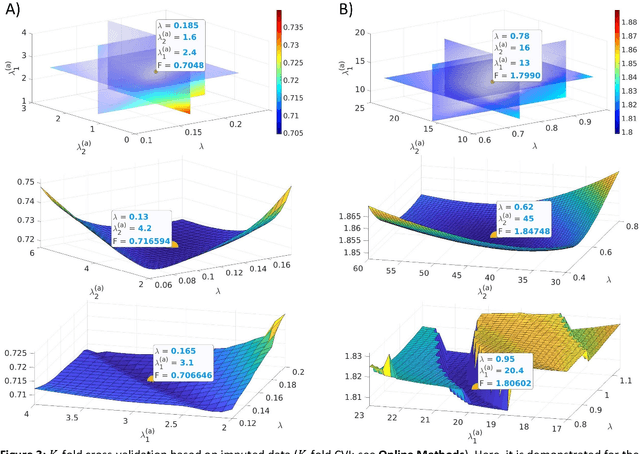
State-space models are used in many fields when dynamics are unobserved. Popular methods such as the Kalman filter and expectation maximization enable estimation of these models but pay a high computational cost in large-scale analysis. In these approaches, sparse inverse covariance estimators can reduce the cost; however, a trade-off between enforced sparsity and increased estimation bias occurs, which demands careful consideration in low signal-to-noise ratio scenarios. We overcome these limitations by 1) Introducing multiple penalized state-space models based on data-driven regularization; 2) Implementing novel algorithms such as backpropagation, state-space gradient descent, and alternating least squares; 3) Proposing an extension of K-fold cross-validation to evaluate the regularization parameters. Finally, we solve the simultaneous brain source localization and functional connectivity problems for simulated and real MEG/EEG signals for thousands of sources on the cortical surface, demonstrating a substantial improvement over state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge