Solving hybrid machine learning tasks by traversing weight space geodesics
Paper and Code
Jun 05, 2021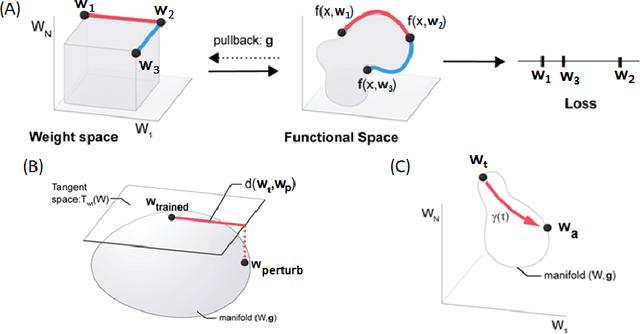
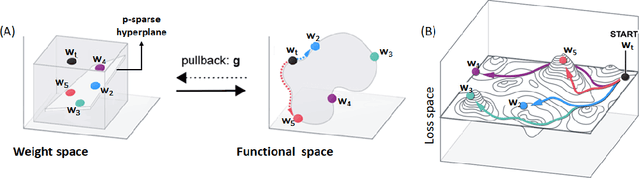
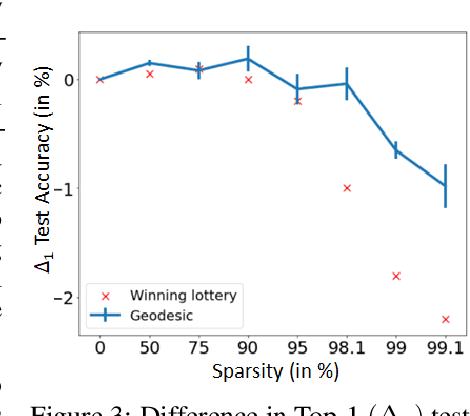
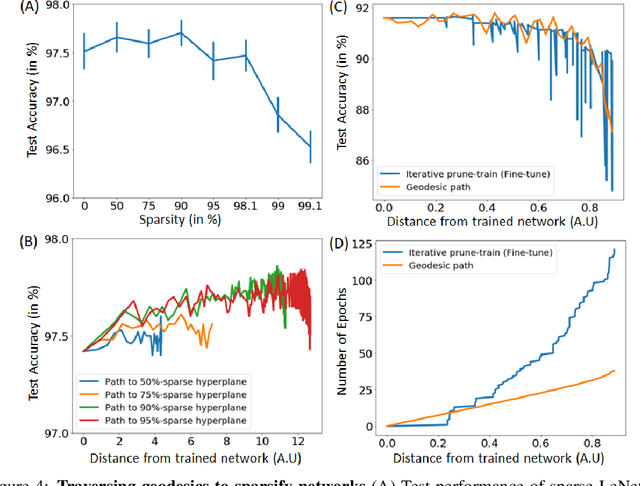
Machine learning problems have an intrinsic geometric structure as central objects including a neural network's weight space and the loss function associated with a particular task can be viewed as encoding the intrinsic geometry of a given machine learning problem. Therefore, geometric concepts can be applied to analyze and understand theoretical properties of machine learning strategies as well as to develop new algorithms. In this paper, we address three seemingly unrelated open questions in machine learning by viewing them through a unified framework grounded in differential geometry. Specifically, we view the weight space of a neural network as a manifold endowed with a Riemannian metric that encodes performance on specific tasks. By defining a metric, we can construct geodesic, minimum length, paths in weight space that represent sets of networks of equivalent or near equivalent functional performance on a specific task. We, then, traverse geodesic paths while identifying networks that satisfy a second objective. Inspired by the geometric insight, we apply our geodesic framework to 3 major applications: (i) Network sparsification (ii) Mitigating catastrophic forgetting by constructing networks with high performance on a series of objectives and (iii) Finding high-accuracy paths connecting distinct local optima of deep networks in the non-convex loss landscape. Our results are obtained on a wide range of network architectures (MLP, VGG11/16) trained on MNIST, CIFAR-10/100. Broadly, we introduce a geometric framework that unifies a range of machine learning objectives and that can be applied to multiple classes of neural network architectures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge