Solving Cosserat Rod Models via Collocation and the Magnus Expansion
Paper and Code
Aug 11, 2020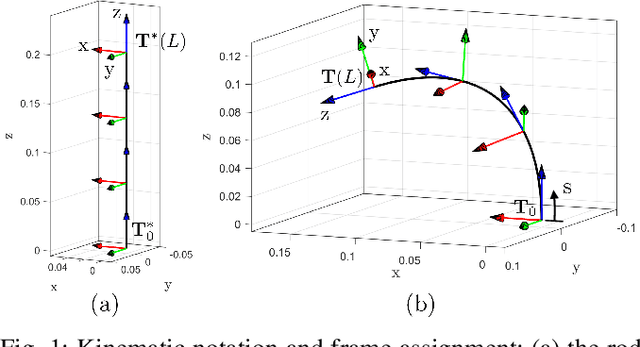
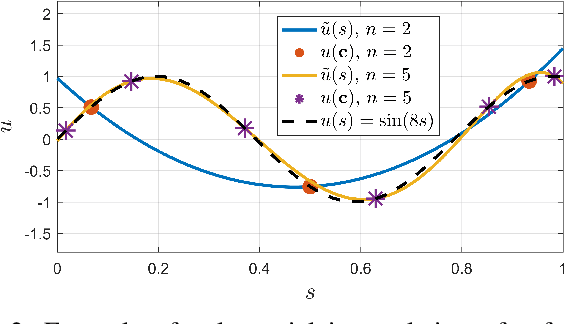
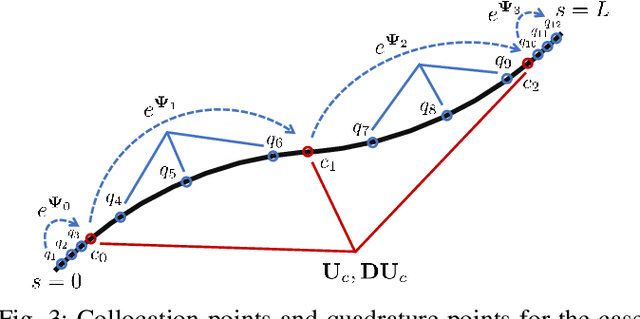
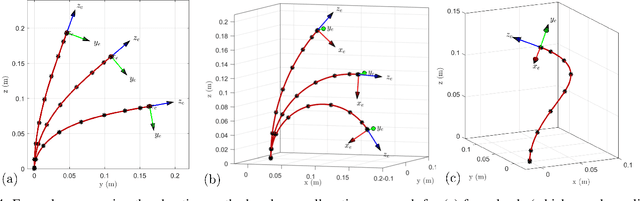
Choosing a kinematic model for a continuum robot typically involves making a tradeoff between accuracy and computational complexity. One common modeling approach is to use the Cosserat rod equations, which have been shown to be accurate for many types of continuum robots. This approach, however, still presents significant computational cost, particularly when many Cosserat rods are coupled via kinematic constraints. In this work, we propose a numerical method that combines orthogonal collocation on the local rod curvature and forward integration of the Cosserat rod kinematic equations via the Magnus expansion, allowing the equilibrium shape to be written as a product of matrix exponentials. We provide a bound on the maximum step size to guarantee convergence of the Magnus expansion for the case of Cosserat rods, compare in simulation against other approaches, and demonstrate the tradeoffs between speed and accuracy for the fourth and sixth order Magnus expansions as well as for different numbers of collocation points. Our results show that the proposed method can find accurate solutions to the Cosserat rod equations and can potentially be competitive in computation speed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge