Solvable Model for Inheriting the Regularization through Knowledge Distillation
Paper and Code
Dec 02, 2020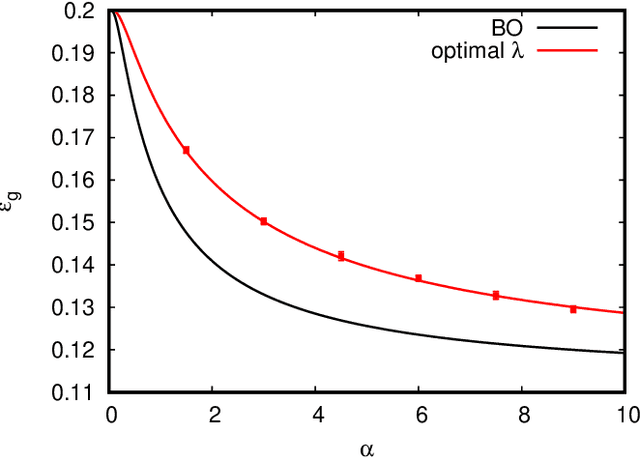
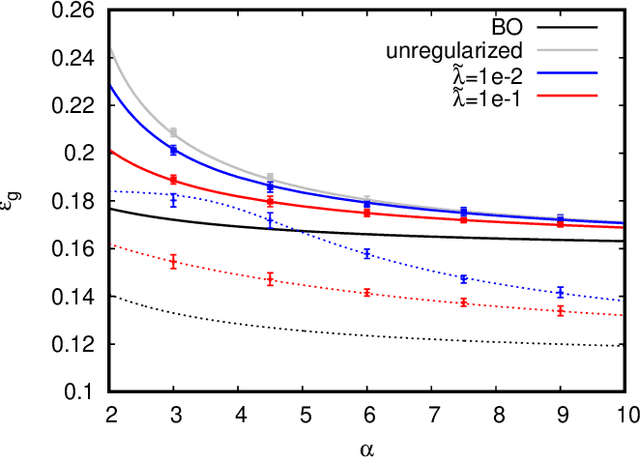
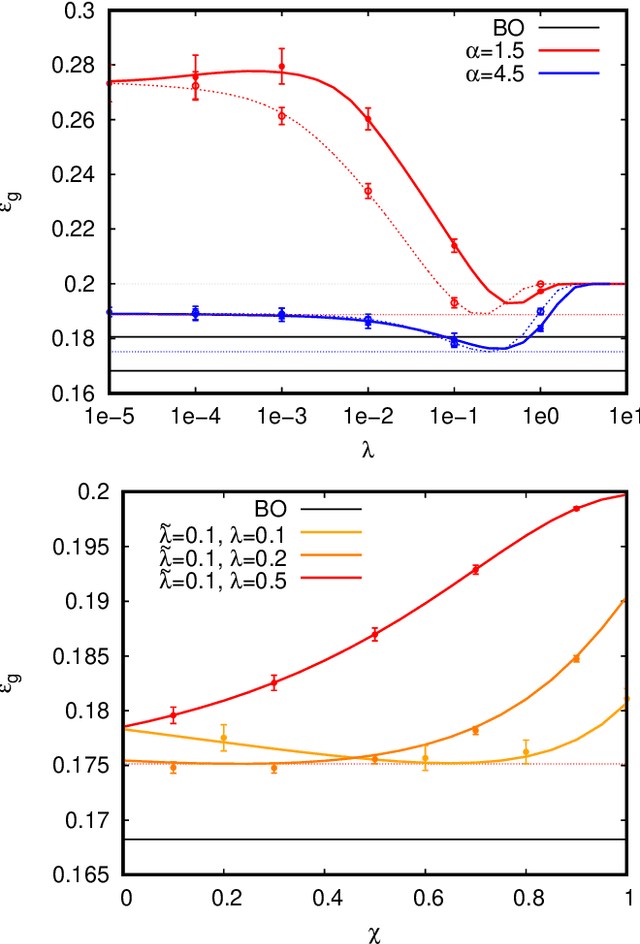
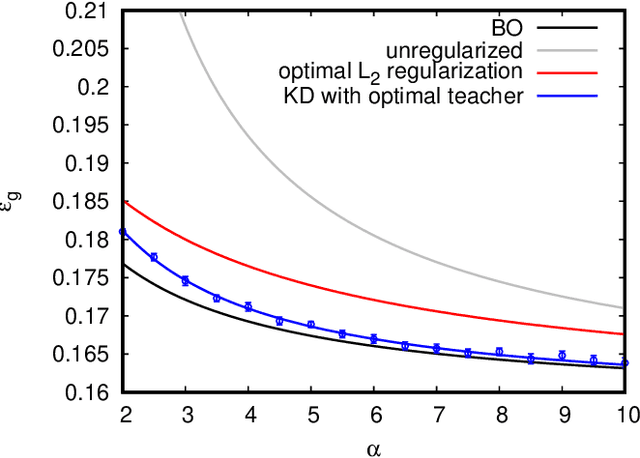
In recent years the empirical success of transfer learning with neural networks has stimulated an increasing interest in obtaining a theoretical understanding of its core properties. Knowledge distillation where a smaller neural network is trained using the outputs of a larger neural network is a particularly interesting case of transfer learning. In the present work, we introduce a statistical physics framework that allows an analytic characterization of the properties of knowledge distillation (KD) in shallow neural networks. Focusing the analysis on a solvable model that exhibits a non-trivial generalization gap, we investigate the effectiveness of KD. We are able to show that, through KD, the regularization properties of the larger teacher model can be inherited by the smaller student and that the yielded generalization performance is closely linked to and limited by the optimality of the teacher. Finally, we analyze the double descent phenomenology that can arise in the considered KD setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge