Solon: Communication-efficient Byzantine-resilient Distributed Training via Redundant Gradients
Paper and Code
Oct 09, 2021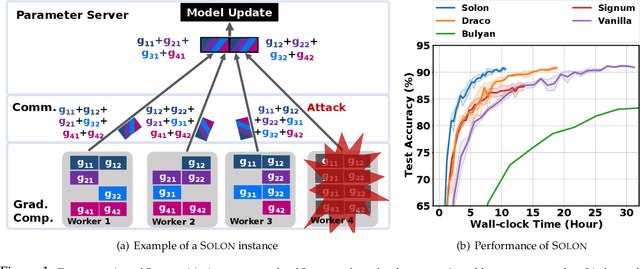
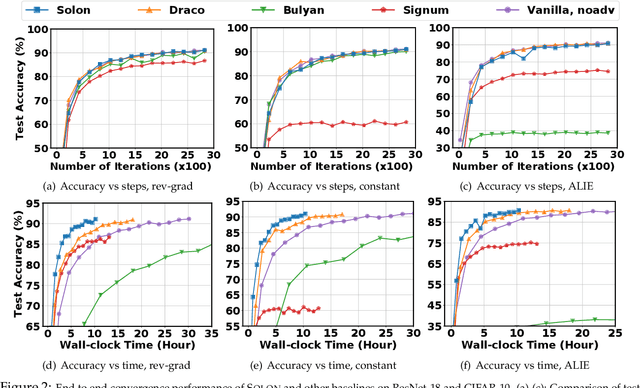

There has been a growing need to provide Byzantine-resilience in distributed model training. Existing robust distributed learning algorithms focus on developing sophisticated robust aggregators at the parameter servers, but pay less attention to balancing the communication cost and robustness. In this paper, we propose Solon, an algorithmic framework that exploits gradient redundancy to provide communication efficiency and Byzantine robustness simultaneously. Our theoretical analysis shows a fundamental trade-off among computational load, communication cost, and Byzantine robustness. We also develop a concrete algorithm to achieve the optimal trade-off, borrowing ideas from coding theory and sparse recovery. Empirical experiments on various datasets demonstrate that Solon provides significant speedups over existing methods to achieve the same accuracy, over 10 times faster than Bulyan and 80% faster than Draco. We also show that carefully designed Byzantine attacks break Signum and Bulyan, but do not affect the successful convergence of Solon.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge