Smoothing Entailment Graphs with Language Models
Paper and Code
Jul 30, 2022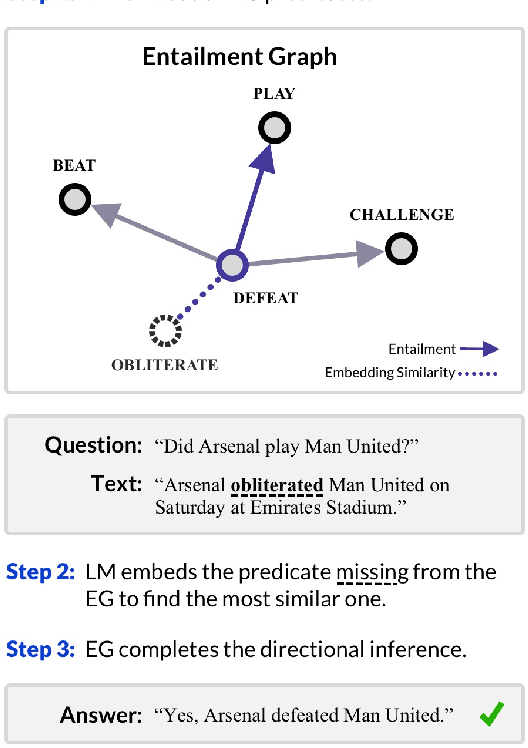


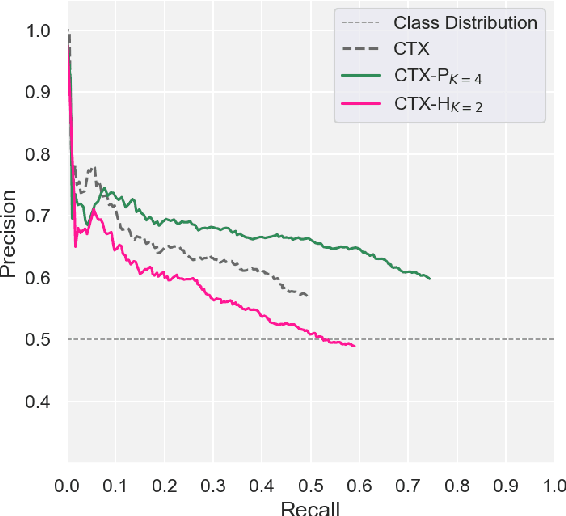
The diversity and Zipfian frequency distribution of natural language predicates in corpora leads to sparsity when learning Entailment Graphs. As symbolic models for natural language inference, an EG cannot recover if missing a novel premise or hypothesis at test-time. In this paper we approach the problem of vertex sparsity by introducing a new method of graph smoothing, using a Language Model to find the nearest approximations of missing predicates. We improve recall by 25.1 and 16.3 absolute percentage points on two difficult directional entailment datasets while exceeding average precision, and show a complementarity with other improvements to edge sparsity. We further analyze language model embeddings and discuss why they are naturally suitable for premise-smoothing, but not hypothesis-smoothing. Finally, we formalize a theory for smoothing a symbolic inference method by constructing transitive chains to smooth both the premise and hypothesis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge