Smooth Sparse Coding via Marginal Regression for Learning Sparse Representations
Paper and Code
Oct 03, 2012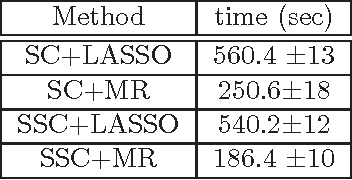


We propose and analyze a novel framework for learning sparse representations, based on two statistical techniques: kernel smoothing and marginal regression. The proposed approach provides a flexible framework for incorporating feature similarity or temporal information present in data sets, via non-parametric kernel smoothing. We provide generalization bounds for dictionary learning using smooth sparse coding and show how the sample complexity depends on the L1 norm of kernel function used. Furthermore, we propose using marginal regression for obtaining sparse codes, which significantly improves the speed and allows one to scale to large dictionary sizes easily. We demonstrate the advantages of the proposed approach, both in terms of accuracy and speed by extensive experimentation on several real data sets. In addition, we demonstrate how the proposed approach could be used for improving semi-supervised sparse coding.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge