Smooth Contextual Bandits: Bridging the Parametric and Non-differentiable Regret Regimes

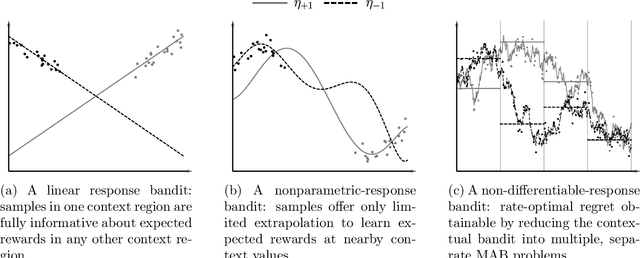
We study a nonparametric contextual bandit problem where the expected reward functions belong to a H\"older class with smoothness parameter $\beta$. We show how this interpolates between two extremes that were previously studied in isolation: non-differentiable bandits ($\beta\leq1$), where rate-optimal regret is achieved by running separate non-contextual bandits in different context regions, and parametric-response bandits ($\beta=\infty$), where rate-optimal regret can be achieved with minimal or no exploration due to infinite extrapolatability. We develop a novel algorithm that carefully adjusts to all smoothness settings and we prove its regret is rate-optimal by establishing matching upper and lower bounds, recovering the existing results at the two extremes. In this sense, our work bridges the gap between the existing literature on parametric and non-differentiable contextual bandit problems and between bandit algorithms that exclusively use global or local information, shedding light on the crucial interplay of complexity and regret in contextual bandits.