Sliced Score Matching: A Scalable Approach to Density and Score Estimation

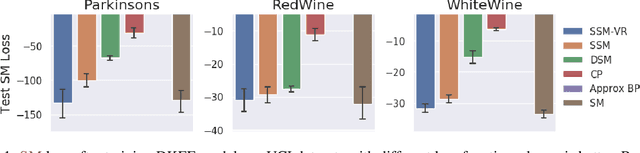
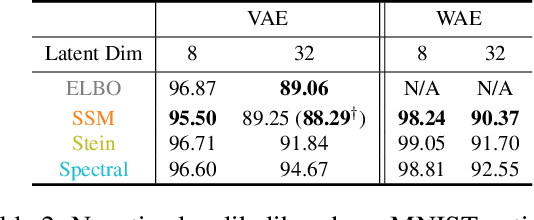
Score matching is a popular method for estimating unnormalized statistical models. However, it has been so far limited to simple models or low-dimensional data, due to the difficulty of computing the trace of Hessians for log-density functions. We show this difficulty can be mitigated by sliced score matching, a new objective that matches random projections of the original scores. Our objective only involves Hessian-vector products, which can be easily implemented using reverse-mode auto-differentiation. This enables scalable score matching for complex models and higher dimensional data. Theoretically, we prove the consistency and asymptotic normality of sliced score matching. Moreover, we demonstrate that sliced score matching can be used to learn deep score estimators for implicit distributions. In our experiments, we show that sliced score matching greatly outperforms competitors on learning deep energy-based models, and can produce accurate score estimates for applications such as variational inference with implicit distributions and training Wasserstein Auto-Encoders.