sKPNSGA-II: Knee point based MOEA with self-adaptive angle for Mission Planning Problems
Paper and Code
Feb 20, 2020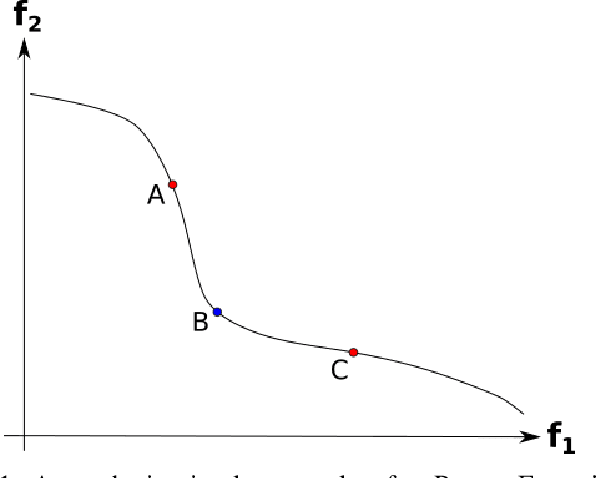
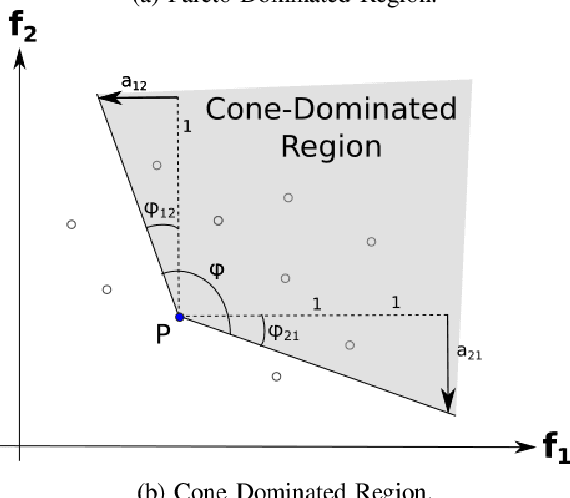
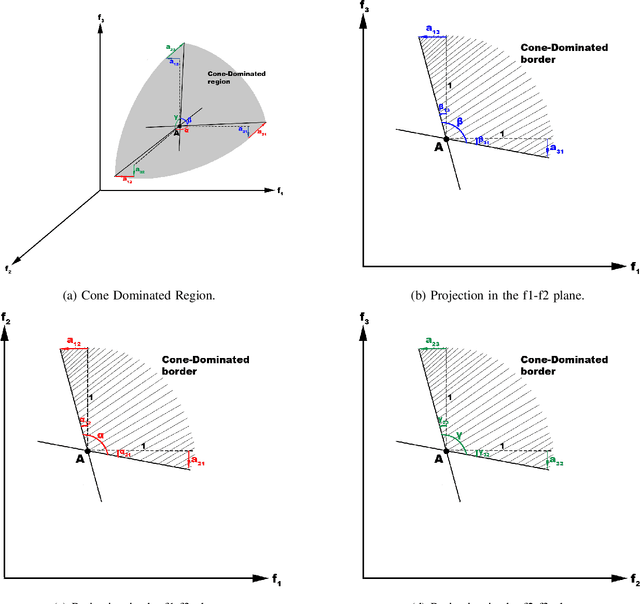
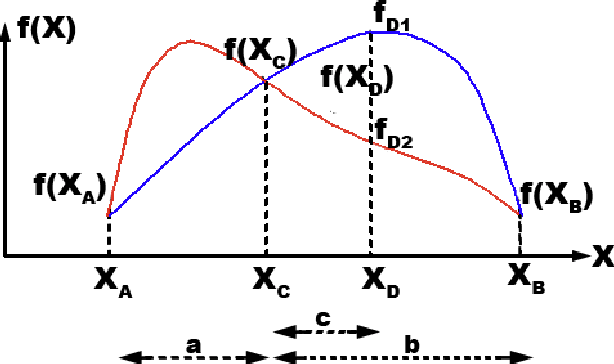
Real-world and complex problems have usually many objective functions that have to be optimized all at once. Over the last decades, Multi-Objective Evolutionary Algorithms (MOEAs) are designed to solve this kind of problems. Nevertheless, some problems have many objectives which lead to a large number of non-dominated solutions obtained by the optimization algorithms. The large set of non-dominated solutions hinders the selection of the most appropriate solution by the decision maker. This paper presents a new algorithm that has been designed to obtain the most significant solutions from the Pareto Optimal Frontier (POF). This approach is based on the cone-domination applied to MOEA, which can find the knee point solutions. In order to obtain the best cone angle, we propose a hypervolume-distribution metric, which is used to self-adapt the angle during the evolving process. This new algorithm has been applied to the real world application in Unmanned Air Vehicle (UAV) Mission Planning Problem. The experimental results show a significant improvement of the algorithm performance in terms of hypervolume, number of solutions, and also the required number of generations to converge.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge