Single photon in hierarchical architecture for physical reinforcement learning: Photon intelligence
Paper and Code
Sep 01, 2016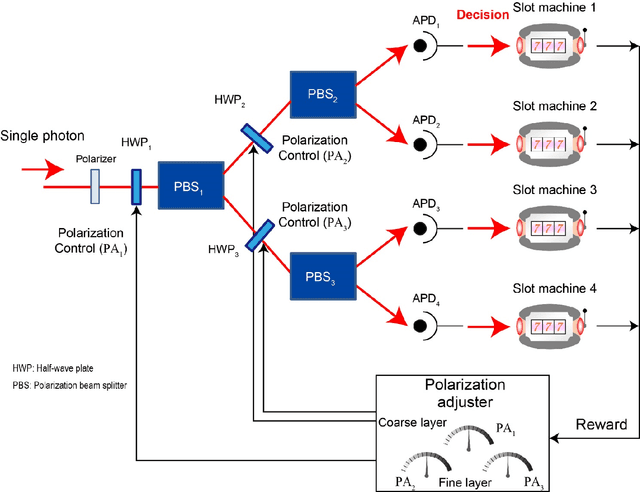



Understanding and using natural processes for intelligent functionalities, referred to as natural intelligence, has recently attracted interest from a variety of fields, including post-silicon computing for artificial intelligence and decision making in the behavioural sciences. In a past study, we successfully used the wave-particle duality of single photons to solve the two-armed bandit problem, which constitutes the foundation of reinforcement learning and decision making. In this study, we propose and confirm a hierarchical architecture for single-photon-based reinforcement learning and decision making that verifies the scalability of the principle. Specifically, the four-armed bandit problem is solved given zero prior knowledge in a two-layer hierarchical architecture, where polarization is autonomously adapted in order to effect adequate decision making using single-photon measurements. In the hierarchical structure, the notion of layer-dependent decisions emerges. The optimal solutions in the coarse layer and in the fine layer, however, conflict with each other in some contradictive problems. We show that while what we call a tournament strategy resolves such contradictions, the probabilistic nature of single photons allows for the direct location of the optimal solution even for contradictive problems, hence manifesting the exploration ability of single photons. This study provides insights into photon intelligence in hierarchical architectures for future artificial intelligence as well as the potential of natural processes for intelligent functionalities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge