Simultaneous Robot-World and Hand-Eye Calibration
Paper and Code
Nov 20, 2023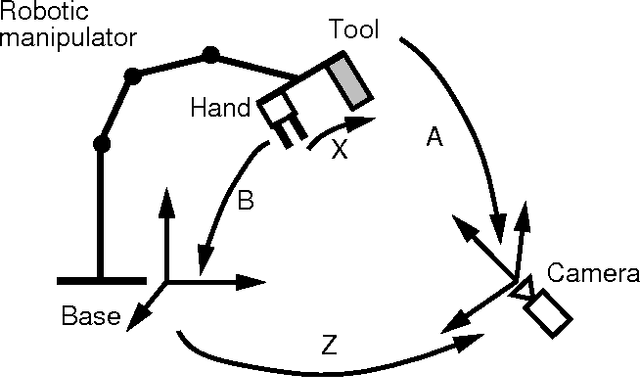
Recently, Zhuang, Roth, \& Sudhakar [1] proposed a method that allows simultaneous computation of the rigid transformations from world frame to robot base frame and from hand frame to camera frame. Their method attempts to solve a homogeneous matrix equation of the form AX=ZB. They use quaternions to derive explicit linear solutions for X and Z. In this short paper, we present two new solutions that attempt to solve the homogeneous matrix equation mentioned above: (i) a closed-form method which uses quaternion algebra and a positive quadratic error function associated with this representation and (ii) a method based on non-linear constrained minimization and which simultaneously solves for rotations and translations. These results may be useful to other problems that can be formulated in the same mathematical form. We perform a sensitivity analysis for both our two methods and the linear method developed by Zhuang et al. This analysis allows the comparison of the three methods. In the light of this comparison the non-linear optimization method, which solves for rotations and translations simultaneously, seems to be the most stable one with respect to noise and to measurement errors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge