Simplicial Complex based Point Correspondence between Images warped onto Manifolds
Paper and Code
Jul 07, 2020


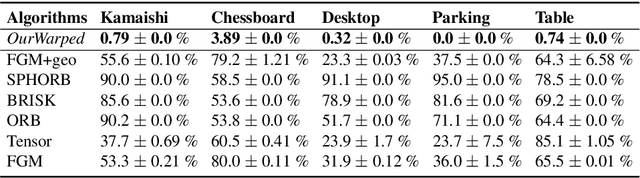
Recent increase in the availability of warped images projected onto a manifold (e.g., omnidirectional spherical images), coupled with the success of higher-order assignment methods, has sparked an interest in the search for improved higher-order matching algorithms on warped images due to projection. Although currently, several existing methods "flatten" such 3D images to use planar graph / hypergraph matching methods, they still suffer from severe distortions and other undesired artifacts, which result in inaccurate matching. Alternatively, current planar methods cannot be trivially extended to effectively match points on images warped onto manifolds. Hence, matching on these warped images persists as a formidable challenge. In this paper, we pose the assignment problem as finding a bijective map between two graph induced simplicial complexes, which are higher-order analogues of graphs. We propose a constrained quadratic assignment problem (QAP) that matches each p-skeleton of the simplicial complexes, iterating from the highest to the lowest dimension. The accuracy and robustness of our approach are illustrated on both synthetic and real-world spherical / warped (projected) images with known ground-truth correspondences. We significantly outperform existing state-of-the-art spherical matching methods on a diverse set of datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge