Signal inference with unknown response: Calibration-uncertainty renormalized estimator
Paper and Code
Mar 02, 2015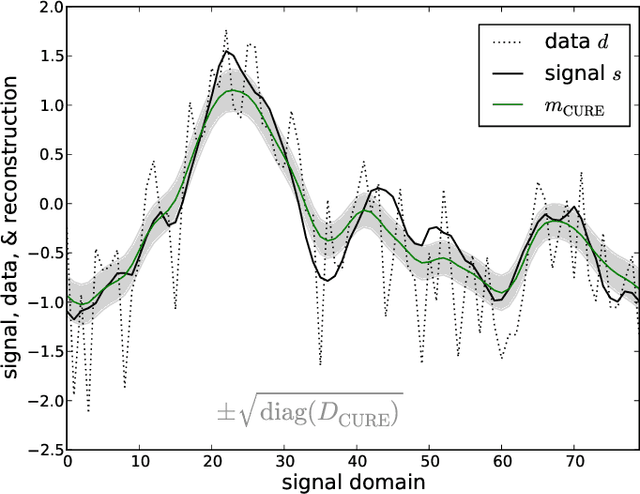
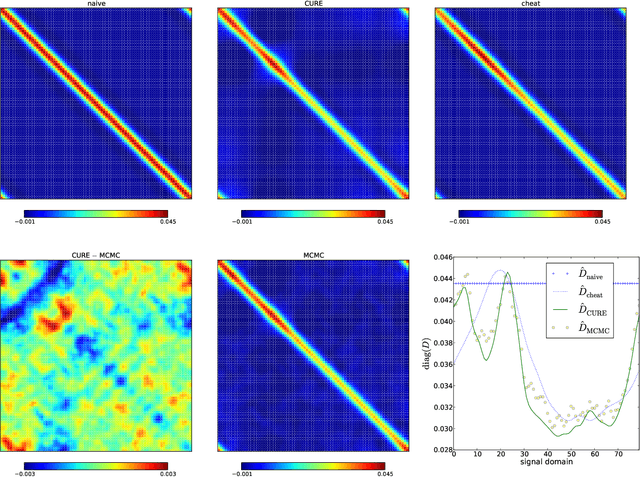
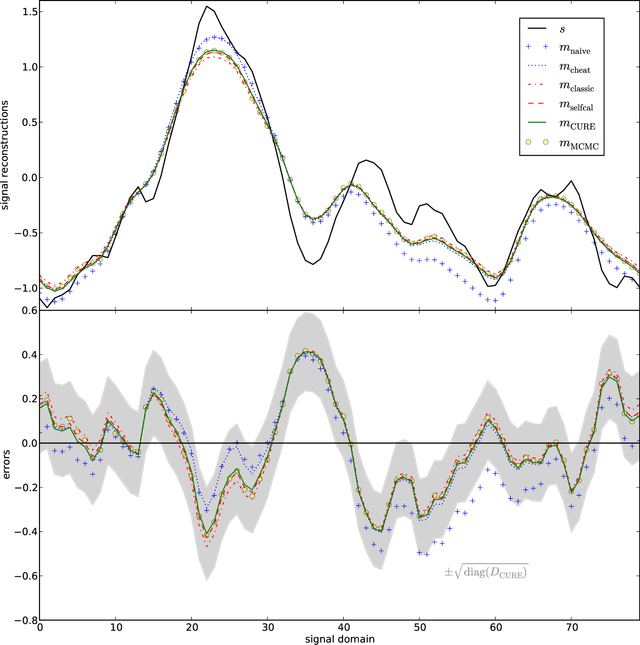
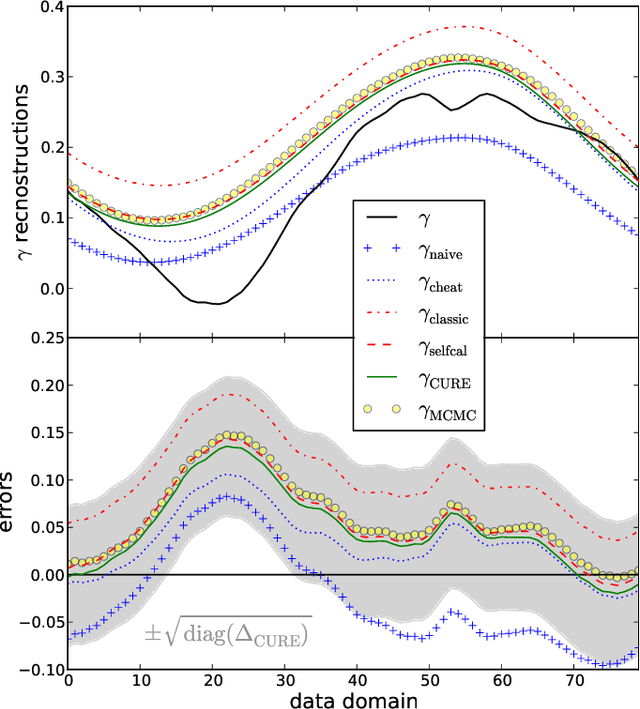
The calibration of a measurement device is crucial for every scientific experiment, where a signal has to be inferred from data. We present CURE, the calibration uncertainty renormalized estimator, to reconstruct a signal and simultaneously the instrument's calibration from the same data without knowing the exact calibration, but its covariance structure. The idea of CURE, developed in the framework of information field theory, is starting with an assumed calibration to successively include more and more portions of calibration uncertainty into the signal inference equations and to absorb the resulting corrections into renormalized signal (and calibration) solutions. Thereby, the signal inference and calibration problem turns into solving a single system of ordinary differential equations and can be identified with common resummation techniques used in field theories. We verify CURE by applying it to a simplistic toy example and compare it against existent self-calibration schemes, Wiener filter solutions, and Markov Chain Monte Carlo sampling. We conclude that the method is able to keep up in accuracy with the best self-calibration methods and serves as a non-iterative alternative to it.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge