SIA-GCN: A Spatial Information Aware Graph Neural Network with 2D Convolutions for Hand Pose Estimation
Paper and Code
Sep 25, 2020
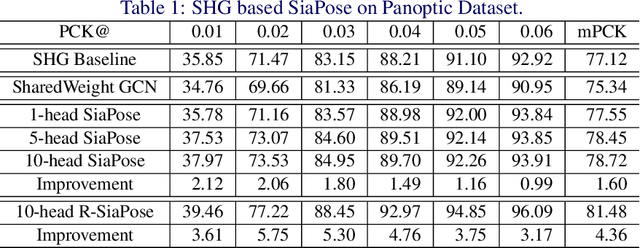
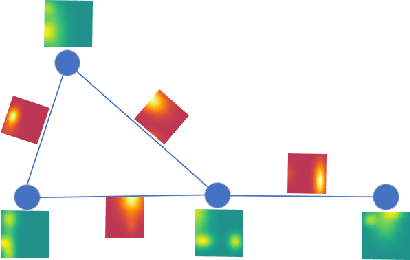
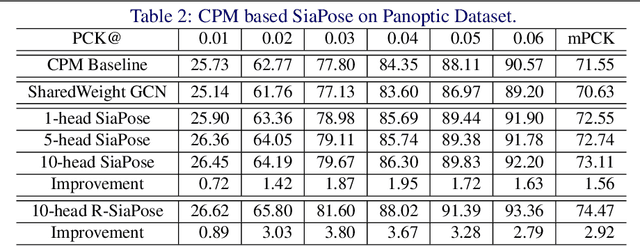
Graph Neural Networks (GNNs) generalize neural networks from applications on regular structures to applications on arbitrary graphs, and have shown success in many application domains such as computer vision, social networks and chemistry. In this paper, we extend GNNs along two directions: a) allowing features at each node to be represented by 2D spatial confidence maps instead of 1D vectors; and b) proposing an efficient operation to integrate information from neighboring nodes through 2D convolutions with different learnable kernels at each edge. The proposed SIA-GCN can efficiently extract spatial information from 2D maps at each node and propagate them through graph convolution. By associating each edge with a designated convolution kernel, the SIA-GCN could capture different spatial relationships for different pairs of neighboring nodes. We demonstrate the utility of SIA-GCN on the task of estimating hand keypoints from single-frame images, where the nodes represent the 2D coordinate heatmaps of keypoints and the edges denote the kinetic relationships between keypoints. Experiments on multiple datasets show that SIA-GCN provides a flexible and yet powerful framework to account for structural constraints between keypoints, and can achieve state-of-the-art performance on the task of hand pose estimation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge