Shuffle Gaussian Mechanism for Differential Privacy

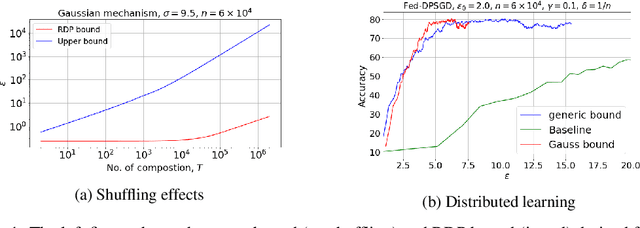
We study Gaussian mechanism in the shuffle model of differential privacy (DP). Particularly, we characterize the mechanism's R\'enyi differential privacy (RDP), showing that it is of the form: $$ \epsilon(\lambda) \leq \frac{1}{\lambda-1}\log\left(\frac{e^{-\lambda/2\sigma^2}}{n^\lambda}\sum_{\substack{k_1+\dotsc+k_n=\lambda;\\k_1,\dotsc,k_n\geq 0}}\binom{\lambda}{k_1,\dotsc,k_n}e^{\sum_{i=1}^nk_i^2/2\sigma^2}\right) $$ We further prove that the RDP is strictly upper-bounded by the Gaussian RDP without shuffling. The shuffle Gaussian RDP is advantageous in composing multiple DP mechanisms, where we demonstrate its improvement over the state-of-the-art approximate DP composition theorems in privacy guarantees of the shuffle model. Moreover, we extend our study to the subsampled shuffle mechanism and the recently proposed shuffled check-in mechanism, which are protocols geared towards distributed/federated learning. Finally, an empirical study of these mechanisms is given to demonstrate the efficacy of employing shuffle Gaussian mechanism under the distributed learning framework to guarantee rigorous user privacy.