Should Algorithms for Random SAT and Max-SAT be Different?
Paper and Code
Nov 02, 2018
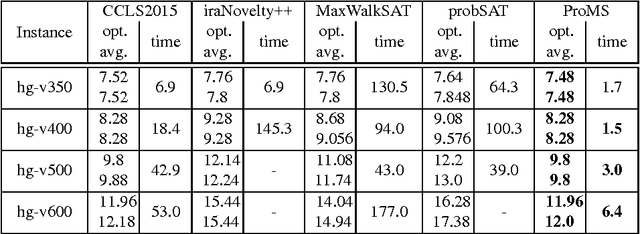

We analyze to what extent the random SAT and Max-SAT problems differ in their properties. Our findings suggest that for random $k$-CNF with ratio in a certain range, Max-SAT can be solved by any SAT algorithm with subexponential slowdown, while for formulae with ratios greater than some constant, algorithms under the random walk framework require substantially different heuristics. In light of these results, we propose a novel probabilistic approach for random Max-SAT called ProMS. Experimental results illustrate that ProMS outperforms many state-of-the-art local search solvers on random Max-SAT benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge