Shedding a PAC-Bayesian Light on Adaptive Sliced-Wasserstein Distances

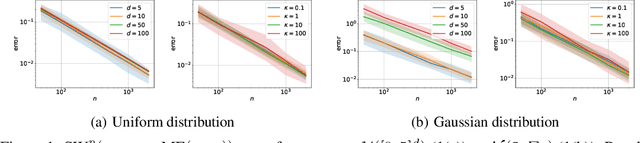
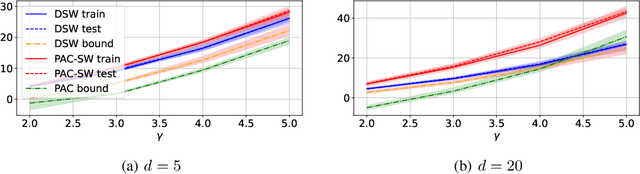
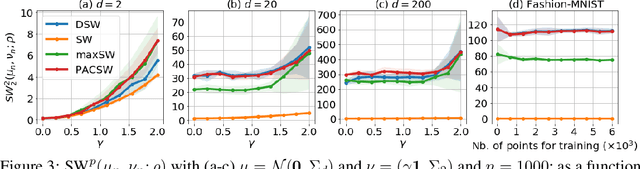
The Sliced-Wasserstein distance (SW) is a computationally efficient and theoretically grounded alternative to the Wasserstein distance. Yet, the literature on its statistical properties with respect to the distribution of slices, beyond the uniform measure, is scarce. To bring new contributions to this line of research, we leverage the PAC-Bayesian theory and the central observation that SW actually hinges on a slice-distribution-dependent Gibbs risk, the kind of quantity PAC-Bayesian bounds have been designed to characterize. We provide four types of results: i) PAC-Bayesian generalization bounds that hold on what we refer as adaptive Sliced-Wasserstein distances, i.e. distances defined with respect to any distribution of slices, ii) a procedure to learn the distribution of slices that yields a maximally discriminative SW, by optimizing our PAC-Bayesian bounds, iii) an insight on how the performance of the so-called distributional Sliced-Wasserstein distance may be explained through our theory, and iv) empirical illustrations of our findings.