Shapley Interpretation and Activation in Neural Networks
Paper and Code
Sep 17, 2019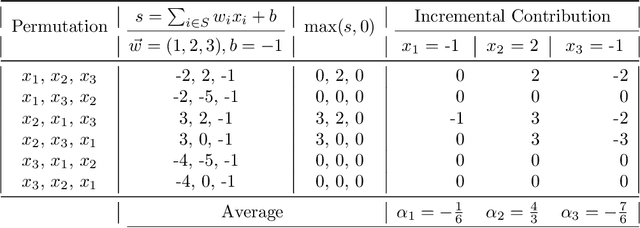
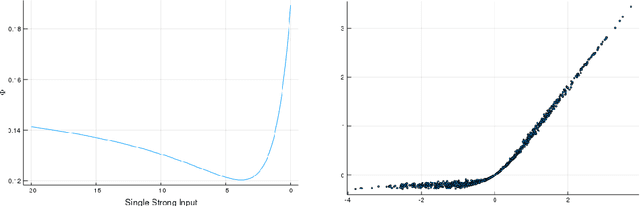
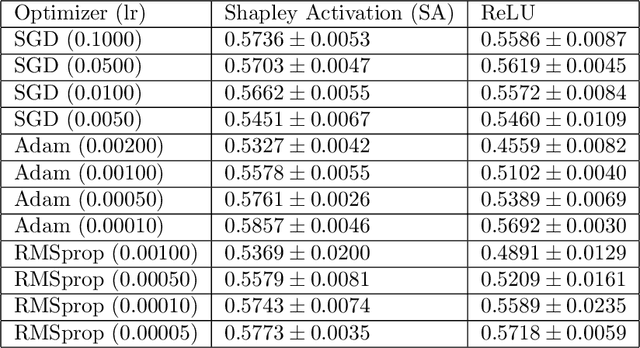
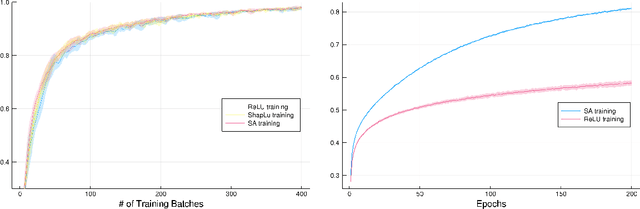
We propose a novel Shapley value approach to help address neural networks' interpretability and "vanishing gradient" problems. Our method is based on an accurate analytical approximation to the Shapley value of a neuron with ReLU activation. This analytical approximation admits a linear propagation of relevance across neural network layers, resulting in a simple, fast and sensible interpretation of neural networks' decision making process. We then derived a globally continuous and non-vanishing Shapley gradient, which can replace the conventional gradient in training neural network layers with ReLU activation, and leading to better training performance. We further derived a Shapley Activation (SA) function, which is a close approximation to ReLU but features the Shapley gradient. The SA is easy to implement in existing machine learning frameworks. Numerical tests show that SA consistently outperforms ReLU in training convergence, accuracy and stability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge