Shape Registration with Directional Data
Paper and Code
Aug 29, 2017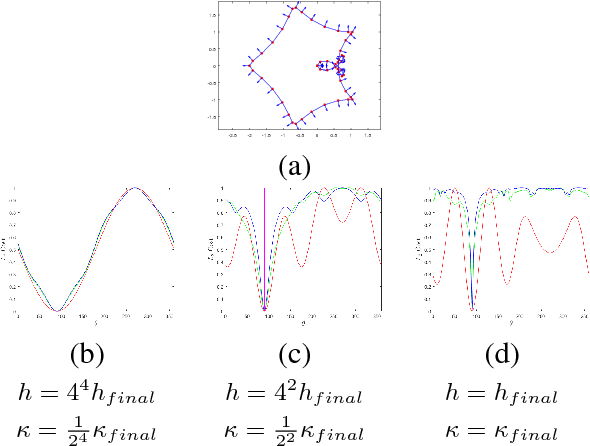
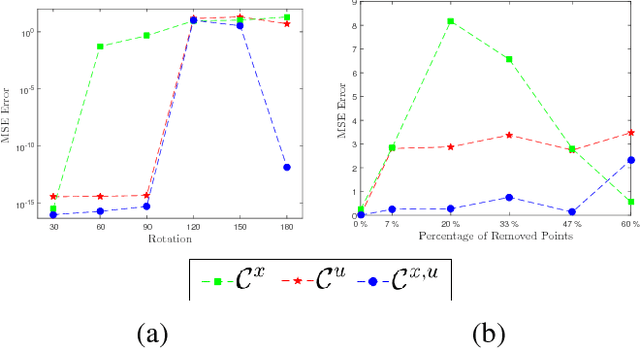
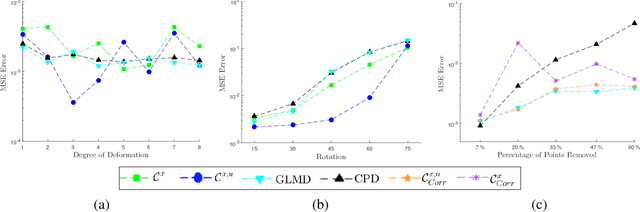
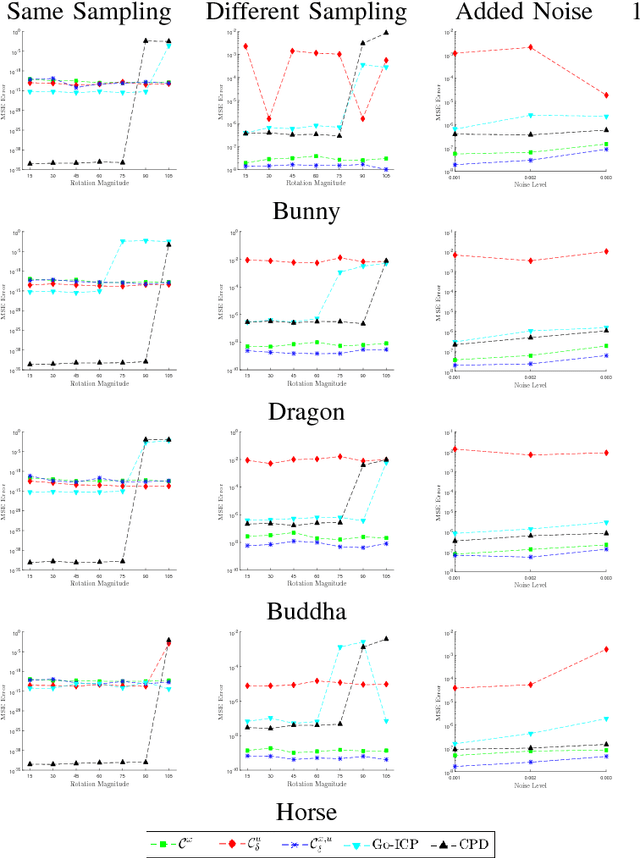
We propose several cost functions for registration of shapes encoded with Euclidean and/or non-Euclidean information (unit vectors). Our framework is assessed for estimation of both rigid and non-rigid transformations between the target and model shapes corresponding to 2D contours and 3D surfaces. The experimental results obtained confirm that using the combination of a point's position and unit normal vector in a cost function can enhance the registration results compared to state of the art methods.
* Pattern Recognition 79 (2018) 452-466 * v2: Updated v1 by adding supplementary material
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge