Shape and Spatially-Varying Reflectance Estimation From Virtual Exemplars
Paper and Code
Sep 21, 2016

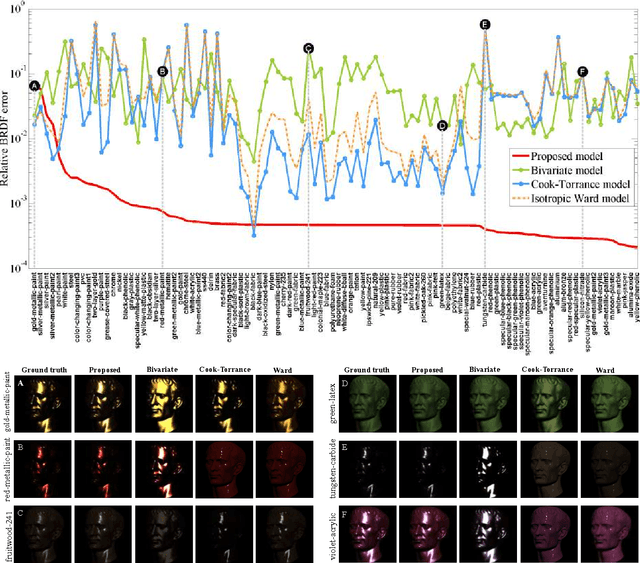

This paper addresses the problem of estimating the shape of objects that exhibit spatially-varying reflectance. We assume that multiple images of the object are obtained under a fixed view-point and varying illumination, i.e., the setting of photometric stereo. At the core of our techniques is the assumption that the BRDF at each pixel lies in the non-negative span of a known BRDF dictionary.This assumption enables a per-pixel surface normal and BRDF estimation framework that is computationally tractable and requires no initialization in spite of the underlying problem being non-convex. Our estimation framework first solves for the surface normal at each pixel using a variant of example-based photometric stereo. We design an efficient multi-scale search strategy for estimating the surface normal and subsequently, refine this estimate using a gradient descent procedure. Given the surface normal estimate, we solve for the spatially-varying BRDF by constraining the BRDF at each pixel to be in the span of the BRDF dictionary, here, we use additional priors to further regularize the solution. A hallmark of our approach is that it does not require iterative optimization techniques nor the need for careful initialization, both of which are endemic to most state-of-the-art techniques. We showcase the performance of our technique on a wide range of simulated and real scenes where we outperform competing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge