SGD Noise and Implicit Low-Rank Bias in Deep Neural Networks
Paper and Code
Jun 12, 2022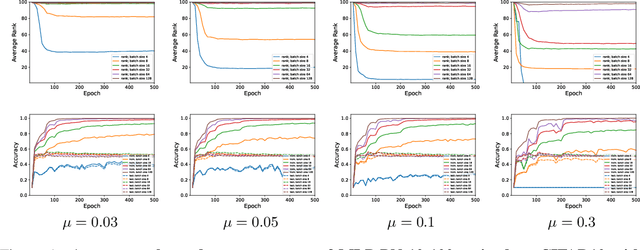
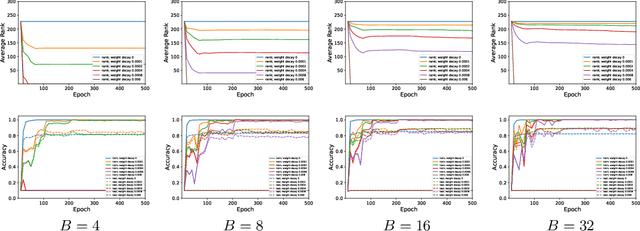
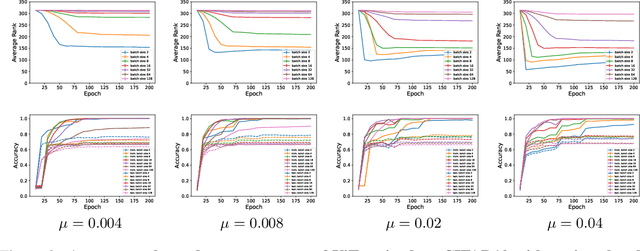
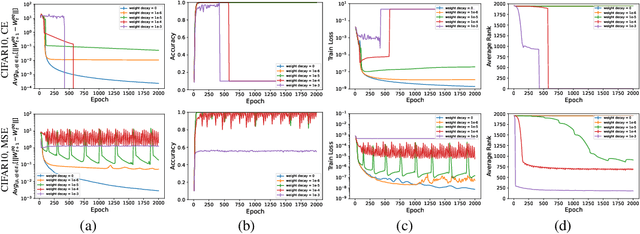
We analyze deep ReLU neural networks trained with mini-batch Stochastic Gradient Descent (SGD) and weight decay. We study the source of SGD noise and prove that when training with weight decay, the only solutions of SGD at convergence are zero functions. Furthermore, we show, both theoretically and empirically, that when training a neural network using SGD with weight decay and small batch size, the resulting weight matrices are expected to be of small rank. Our analysis relies on a minimal set of assumptions and the neural networks may be arbitrarily wide or deep, and may include residual connections, as well as batch normalization layers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge