Sensor Selection by Linear Programming
Paper and Code
Sep 09, 2015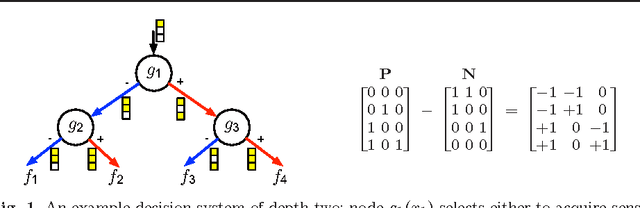

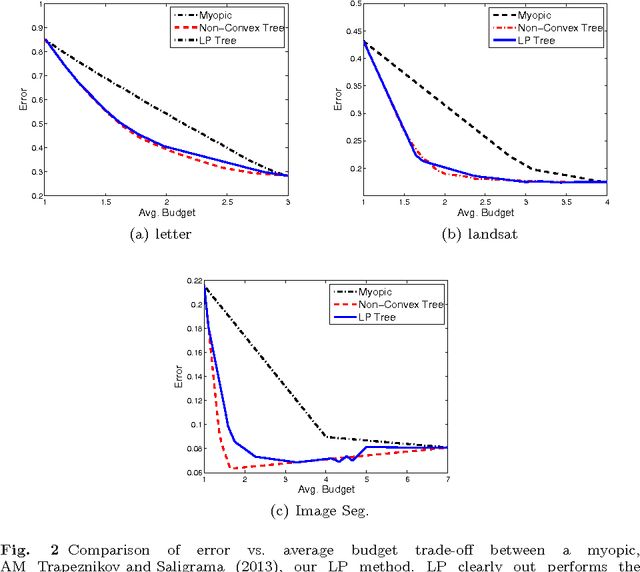

We learn sensor trees from training data to minimize sensor acquisition costs during test time. Our system adaptively selects sensors at each stage if necessary to make a confident classification. We pose the problem as empirical risk minimization over the choice of trees and node decision rules. We decompose the problem, which is known to be intractable, into combinatorial (tree structures) and continuous parts (node decision rules) and propose to solve them separately. Using training data we greedily solve for the combinatorial tree structures and for the continuous part, which is a non-convex multilinear objective function, we derive convex surrogate loss functions that are piecewise linear. The resulting problem can be cast as a linear program and has the advantage of guaranteed convergence, global optimality, repeatability and computational efficiency. We show that our proposed approach outperforms the state-of-art on a number of benchmark datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge