Semi-Supervised Representation Learning based on Probabilistic Labeling
Paper and Code
Sep 15, 2016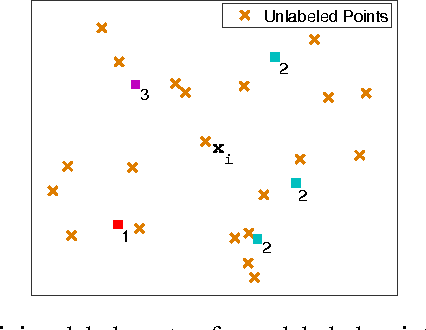
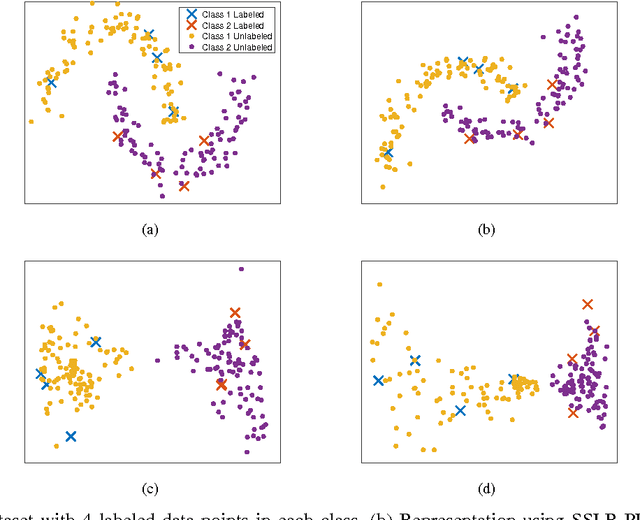
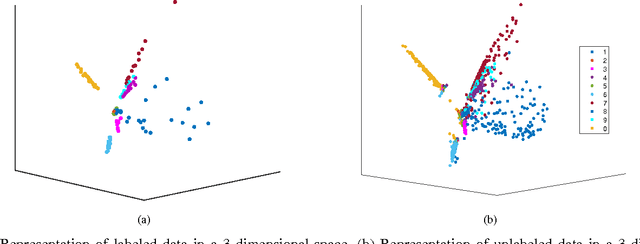
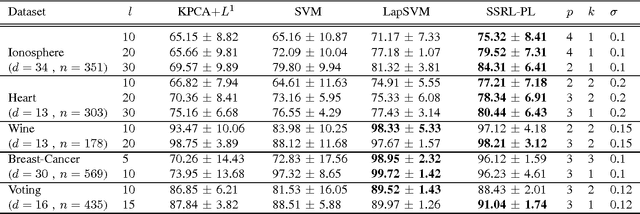
In this paper, we present a new algorithm for semi-supervised representation learning. In this algorithm, we first find a vector representation for the labels of the data points based on their local positions in the space. Then, we map the data to lower-dimensional space using a linear transformation such that the dependency between the transformed data and the assigned labels is maximized. In fact, we try to find a mapping that is as discriminative as possible. The approach will use Hilber-Schmidt Independence Criterion (HSIC) as the dependence measure. We also present a kernelized version of the algorithm, which allows non-linear transformations and provides more flexibility in finding the appropriate mapping. Use of unlabeled data for learning new representation is not always beneficial and there is no algorithm that can deterministically guarantee the improvement of the performance by exploiting unlabeled data. Therefore, we also propose a bound on the performance of the algorithm, which can be used to determine the effectiveness of using the unlabeled data in the algorithm. We demonstrate the ability of the algorithm in finding the transformation using both toy examples and real-world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge