Semi-supervised Invertible DeepONets for Bayesian Inverse Problems
Paper and Code
Sep 08, 2022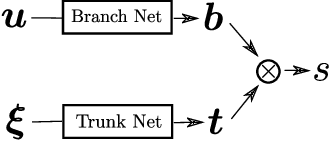
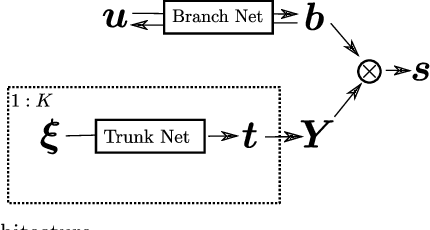


Deep Operator Networks (DeepONets) offer a powerful, data-driven tool for solving parametric PDEs by learning operators, i.e. maps between infinite-dimensional function spaces. In this work, we employ physics-informed DeepONets in the context of high-dimensional, Bayesian inverse problems. Traditional solution strategies necessitate an enormous, and frequently infeasible, number of forward model solves, as well as the computation of parametric derivatives. In order to enable efficient solutions, we extend DeepONets by employing a realNVP architecture which yields an invertible and differentiable map between the parametric input and the branch net output. This allows us to construct accurate approximations of the full posterior which can be readily adapted irrespective of the number of observations and the magnitude of the observation noise. As a result, no additional forward solves are required, nor is there any need for costly sampling procedures. We demonstrate the efficacy and accuracy of the proposed methodology in the context of inverse problems based on a anti-derivative, a reaction-diffusion and a Darcy-flow equation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge