Semi-supervised Embedding Learning for High-dimensional Bayesian Optimization
Paper and Code
May 29, 2020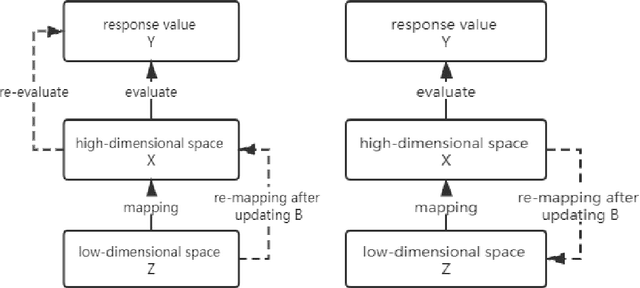
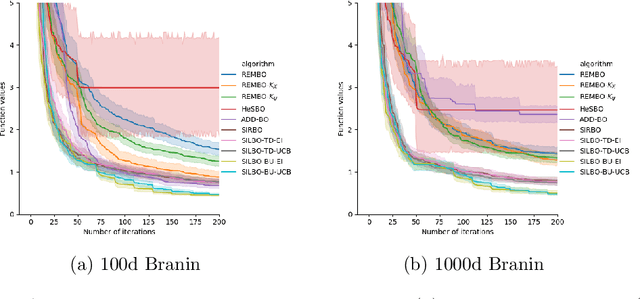
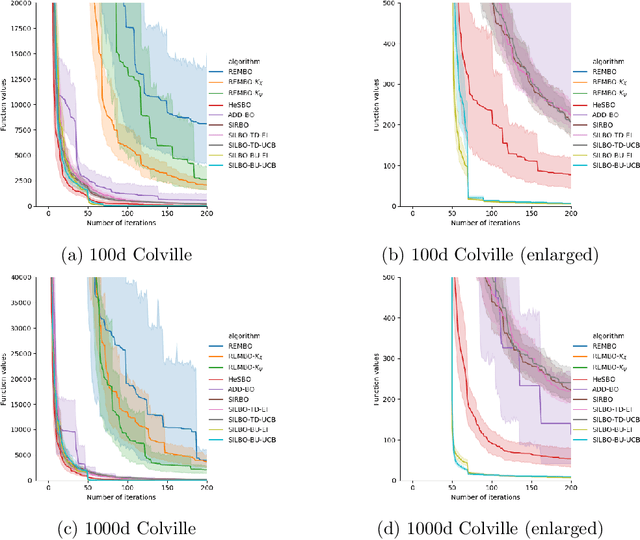
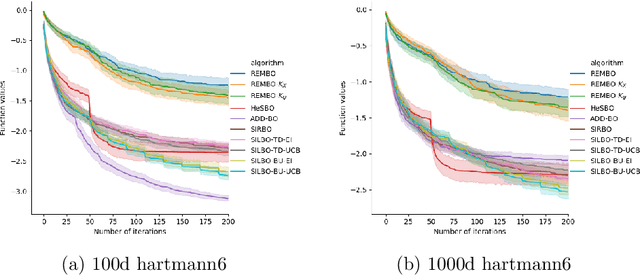
Bayesian optimization is a broadly applied methodology to optimize the expensive black-box function. Despite its success, it still faces the challenge from the high-dimensional search space. To alleviate this problem, we propose a novel Bayesian optimization framework (termed SILBO), which finds a low-dimensional space to perform Bayesian optimization iteratively through semi-supervised dimension reduction. SILBO incorporates both labeled points and unlabeled points acquired from the acquisition function to guide the embedding space learning. To accelerate the learning procedure, we present a randomized method for generating the projection matrix. Furthermore, to map from the low-dimensional space to the high-dimensional original space, we propose two mapping strategies: $\text{SILBO}_{FZ}$ and $\text{SILBO}_{FX}$ according to the evaluation overhead of the objective function. Experimental results on both synthetic function and hyperparameter optimization tasks demonstrate that SILBO outperforms the existing state-of-the-art high-dimensional Bayesian optimization methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge