Semi-supervised Community Detection via Structural Similarity Metrics
Paper and Code
Jun 01, 2023
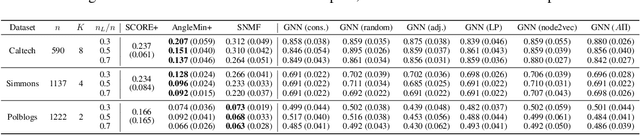


Motivated by social network analysis and network-based recommendation systems, we study a semi-supervised community detection problem in which the objective is to estimate the community label of a new node using the network topology and partially observed community labels of existing nodes. The network is modeled using a degree-corrected stochastic block model, which allows for severe degree heterogeneity and potentially non-assortative communities. We propose an algorithm that computes a `structural similarity metric' between the new node and each of the $K$ communities by aggregating labeled and unlabeled data. The estimated label of the new node corresponds to the value of $k$ that maximizes this similarity metric. Our method is fast and numerically outperforms existing semi-supervised algorithms. Theoretically, we derive explicit bounds for the misclassification error and show the efficiency of our method by comparing it with an ideal classifier. Our findings highlight, to the best of our knowledge, the first semi-supervised community detection algorithm that offers theoretical guarantees.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge