Semantic Interpolation in Implicit Models
Paper and Code
Feb 02, 2018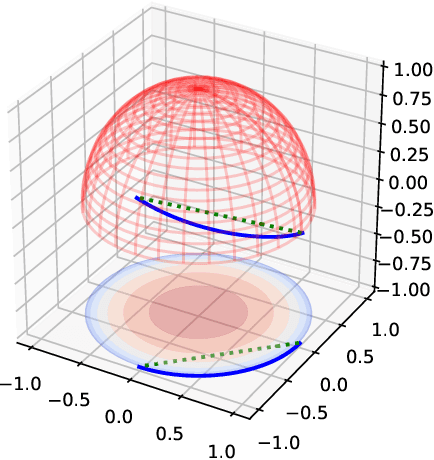
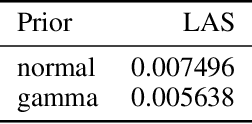
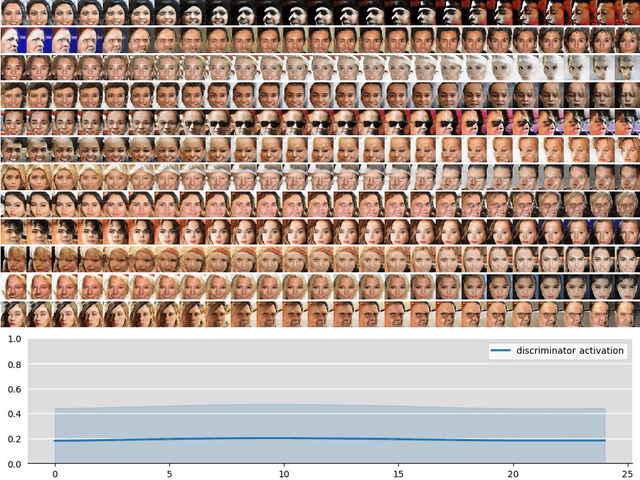

In implicit models, one often interpolates between sampled points in latent space. As we show in this paper, care needs to be taken to match-up the distributional assumptions on code vectors with the geometry of the interpolating paths. Otherwise, typical assumptions about the quality and semantics of in-between points may not be justified. Based on our analysis we propose to modify the prior code distribution to put significantly more probability mass closer to the origin. As a result, linear interpolation paths are not only shortest paths, but they are also guaranteed to pass through high-density regions, irrespective of the dimensionality of the latent space. Experiments on standard benchmark image datasets demonstrate clear visual improvements in the quality of the generated samples and exhibit more meaningful interpolation paths.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge