Self-Supervised Robust Scene Flow Estimation via the Alignment of Probability Density Functions
Paper and Code
Mar 23, 2022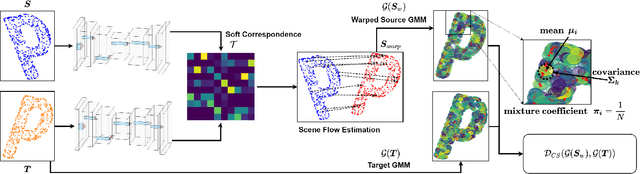
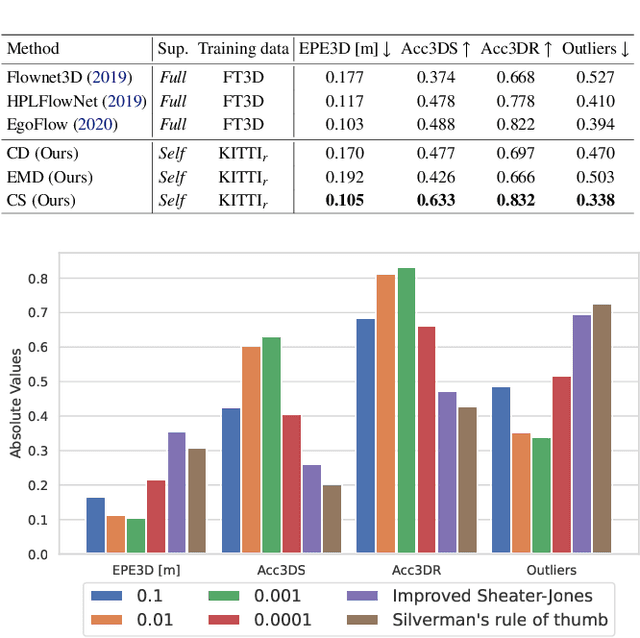
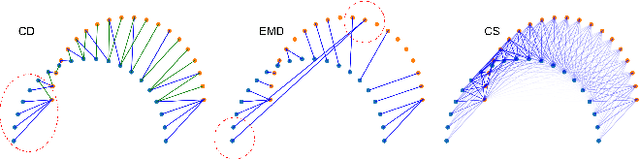
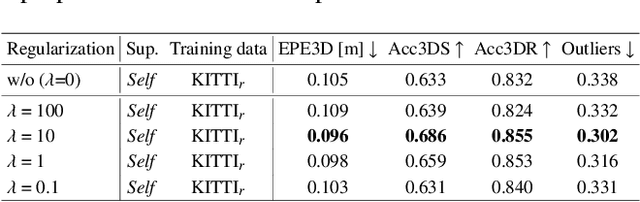
In this paper, we present a new self-supervised scene flow estimation approach for a pair of consecutive point clouds. The key idea of our approach is to represent discrete point clouds as continuous probability density functions using Gaussian mixture models. Scene flow estimation is therefore converted into the problem of recovering motion from the alignment of probability density functions, which we achieve using a closed-form expression of the classic Cauchy-Schwarz divergence. Unlike existing nearest-neighbor-based approaches that use hard pairwise correspondences, our proposed approach establishes soft and implicit point correspondences between point clouds and generates more robust and accurate scene flow in the presence of missing correspondences and outliers. Comprehensive experiments show that our method makes noticeable gains over the Chamfer Distance and the Earth Mover's Distance in real-world environments and achieves state-of-the-art performance among self-supervised learning methods on FlyingThings3D and KITTI, even outperforming some supervised methods with ground truth annotations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge