Self-Filtering: A Noise-Aware Sample Selection for Label Noise with Confidence Penalization
Paper and Code
Aug 24, 2022
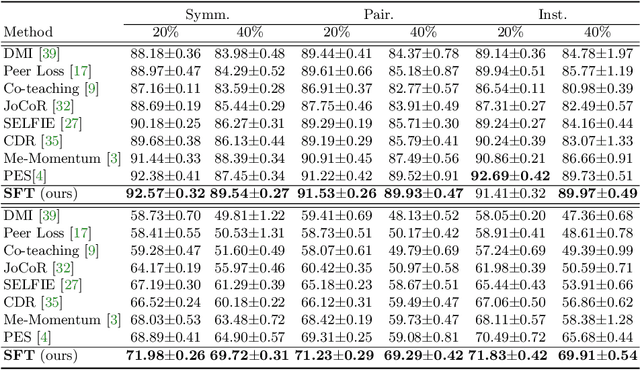
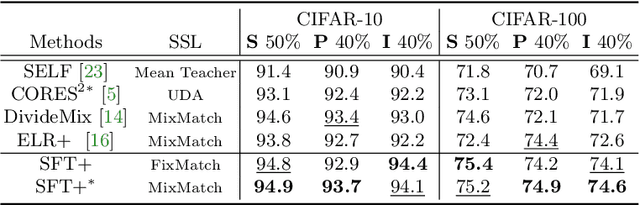
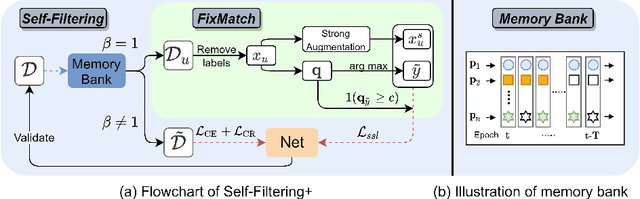
Sample selection is an effective strategy to mitigate the effect of label noise in robust learning. Typical strategies commonly apply the small-loss criterion to identify clean samples. However, those samples lying around the decision boundary with large losses usually entangle with noisy examples, which would be discarded with this criterion, leading to the heavy degeneration of the generalization performance. In this paper, we propose a novel selection strategy, \textbf{S}elf-\textbf{F}il\textbf{t}ering (SFT), that utilizes the fluctuation of noisy examples in historical predictions to filter them, which can avoid the selection bias of the small-loss criterion for the boundary examples. Specifically, we introduce a memory bank module that stores the historical predictions of each example and dynamically updates to support the selection for the subsequent learning iteration. Besides, to reduce the accumulated error of the sample selection bias of SFT, we devise a regularization term to penalize the confident output distribution. By increasing the weight of the misclassified categories with this term, the loss function is robust to label noise in mild conditions. We conduct extensive experiments on three benchmarks with variant noise types and achieve the new state-of-the-art. Ablation studies and further analysis verify the virtue of SFT for sample selection in robust learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge