Self-Dictionary Sparse Regression for Hyperspectral Unmixing: Greedy Pursuit and Pure Pixel Search are Related
Paper and Code
Mar 03, 2015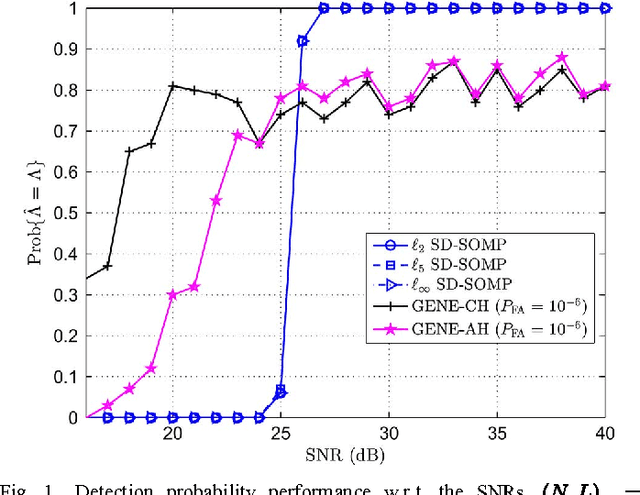
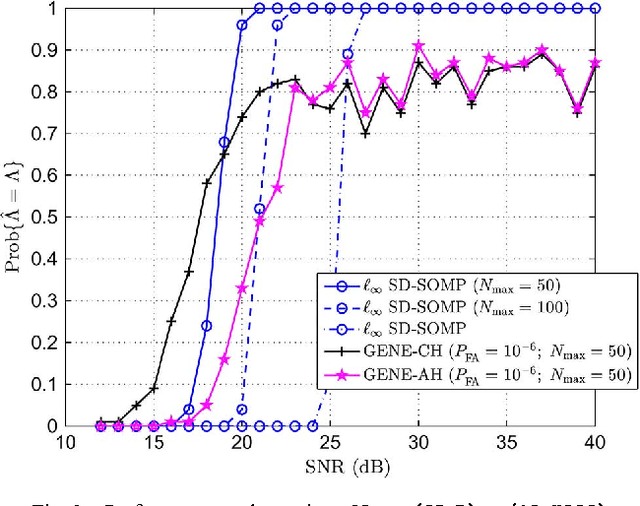
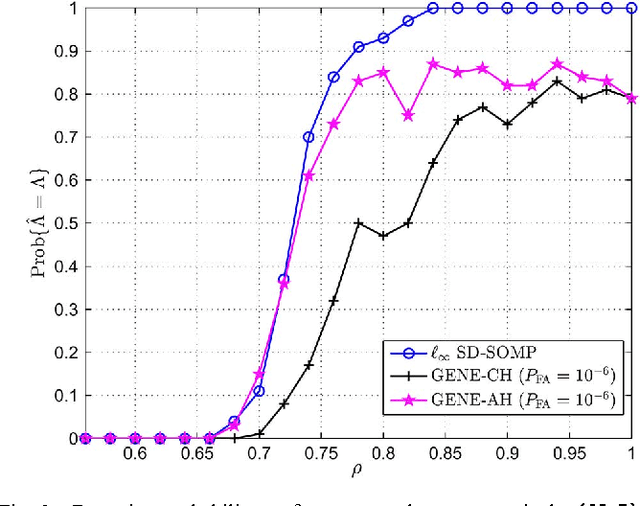
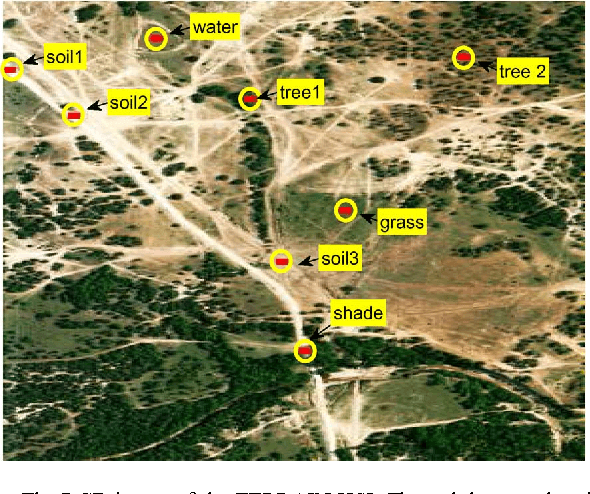
This paper considers a recently emerged hyperspectral unmixing formulation based on sparse regression of a self-dictionary multiple measurement vector (SD-MMV) model, wherein the measured hyperspectral pixels are used as the dictionary. Operating under the pure pixel assumption, this SD-MMV formalism is special in that it allows simultaneous identification of the endmember spectral signatures and the number of endmembers. Previous SD-MMV studies mainly focus on convex relaxations. In this study, we explore the alternative of greedy pursuit, which generally provides efficient and simple algorithms. In particular, we design a greedy SD-MMV algorithm using simultaneous orthogonal matching pursuit. Intriguingly, the proposed greedy algorithm is shown to be closely related to some existing pure pixel search algorithms, especially, the successive projection algorithm (SPA). Thus, a link between SD-MMV and pure pixel search is revealed. We then perform exact recovery analyses, and prove that the proposed greedy algorithm is robust to noise---including its identification of the (unknown) number of endmembers---under a sufficiently low noise level. The identification performance of the proposed greedy algorithm is demonstrated through both synthetic and real-data experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge