Selective Inference for $L_2$-Boosting

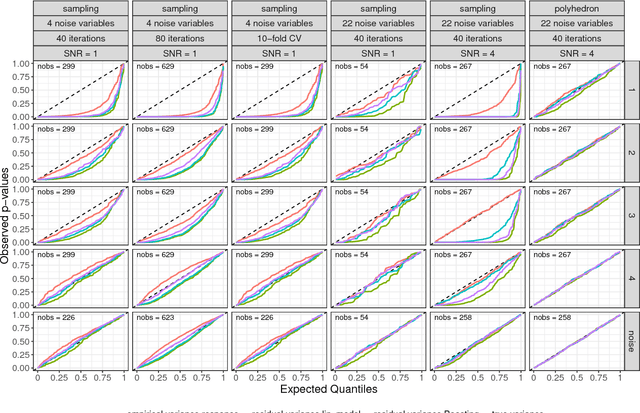
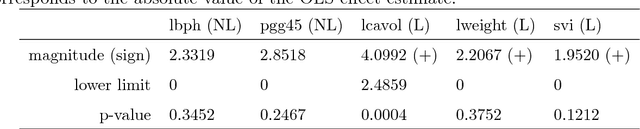
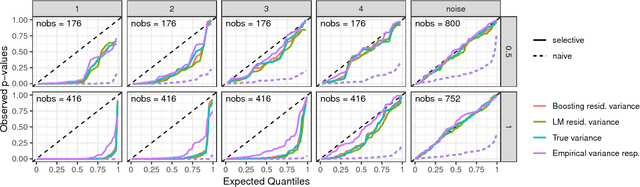
We adapt and extend several recent proposals for post-selection inference to transfer them to the component-wise functional gradient descent algorithm (CFGD) under normality assumption for model errors, also known as $L_2$-Boosting. The CFGD is one of the most versatile toolboxes to analyze data as it scales well to high-dimensional data sets, allows for a very flexible definition of additive regression models and incorporates inbuilt variable selection. Due to the iterative nature, which can repeatedly select the same component to update, a statistical inference framework for component-wise boosting algorithms requires adaptations of existing approaches; we propose tests and confidence intervals for linear, grouped and penalized additive model components selected by $L_2$-Boosting. Our concepts also transfer to slow-learning algorithms and to other selection techniques which restrict the response space to more complex sets than polyhedra. We apply our framework to an additive model for the prostate cancer data set to compare with previous results, and investigate the properties of our concepts in simulation studies.