Seeking multi-thresholds for image segmentation with Learning Automata
Paper and Code
May 28, 2014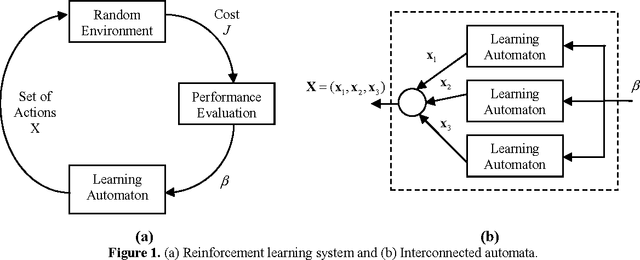


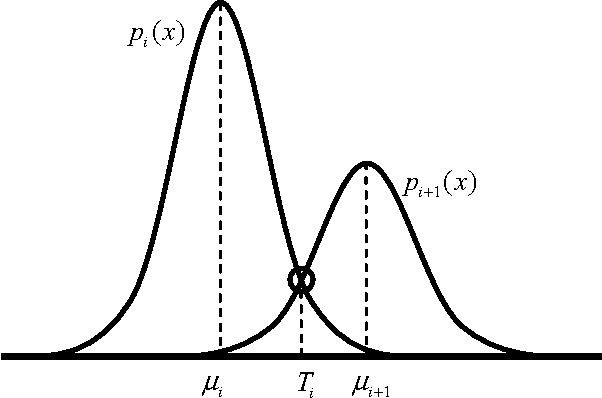
This paper explores the use of the Learning Automata (LA) algorithm to compute threshold selection for image segmentation as it is a critical preprocessing step for image analysis, pattern recognition and computer vision. LA is a heuristic method which is able to solve complex optimization problems with interesting results in parameter estimation. Despite other techniques commonly seek through the parameter map, LA explores in the probability space providing appropriate convergence properties and robustness. The segmentation task is therefore considered as an optimization problem and the LA is used to generate the image multi-threshold separation. In this approach, one 1D histogram of a given image is approximated through a Gaussian mixture model whose parameters are calculated using the LA algorithm. Each Gaussian function approximating the histogram represents a pixel class and therefore a threshold point. The method shows fast convergence avoiding the typical sensitivity to initial conditions such as the Expectation Maximization (EM) algorithm or the complex time-consuming computations commonly found in gradient methods. Experimental results demonstrate the algorithm ability to perform automatic multi-threshold selection and show interesting advantages as it is compared to other algorithms solving the same task.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge